BINOMIAL THEOREM

Binomial theorem facilitates the algebraic expansion of the binomial (a + b) for a positive integral exponent n. Binomial theorem is used in all branches of Mathematics and also in other Sciences. Using the theorem, for example one can easily find the coefficient of x²⁰ in the expansion of (2x - 7)²³. 

If one wants to know the maturity amount after 10 years on a sum of money deposited in a bank at the rate of 8% compound interest per year or to know the size of population of our country after 15 years if the annual growth rate and present population size are known,

Binomial theorem helps us in finding the above quantities. The coefficients that appear in the binomial expansion of (a + b)ⁿ, n ∈ N, are called binomial coefficients. Binomial theorem plays a vital role in determining the probabilities of events when the random experiment involves finite sample space and each outcome is either success or failure

Binomial Theorem

The binomial theorem states the principle for expanding the binomial (x + y)ⁿ and expresses it as a sum of the terms involving individual exponents of variables x and y. Each term in a binomial expansion is associated with a numeric value which is called coefficient.

Pascal Triangle

The Pascal triangle is an arrangement of the values of ⁿC_r in a triangular form. The (k + 1)^st row consists values of

^kC₀, ^kC₁, ^kC₂, ^kC₃, ........^kC_k

In fact, the Pascal triangle is

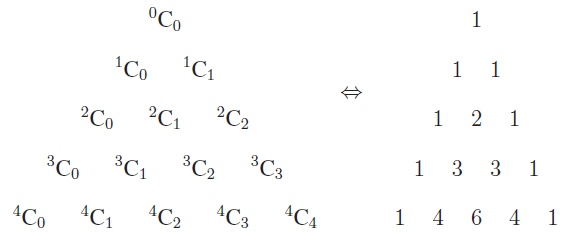
Recall the expansion and observe the coefficients of each term of the identities

(a + b)⁰, (a + b)¹, (a + b)², (a + b)³

There is a pattern in the arrangements of coefficients.

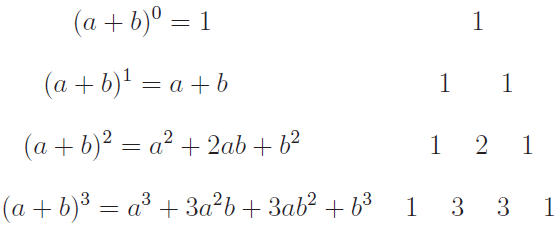
If we observe carefully the Pascal triangle, we may notice that each row starts and ends with 1 and other entries are the sum of the two numbers just above it. For example ‘3’ is the sum of 1 and 2 above it; ‘10’ is the sum of 4 and 6 above it. We will prove in a short while that

(x + y)ⁿ = ⁿC₀xⁿ + ⁿC₁x^n-1y¹ + ⁿC₂x^n-2y² + ⁿC₃x^n-3y³.............  ...................+ ⁿC_rx^n-ry^r + ........ ⁿC_nyⁿ

which is the binomial expansion of (a + b)ⁿ. The binomial expansion of (a + b)ⁿ for any n ∈ N can be written using Pascal triangle. For example, from the fifth row we can write down the expansion of (a + b)⁴ and from the sixth row we can write down the expansion of (a + b)⁵ and so on.

We know the terms (without coefficients) of (a + b)⁵ are

a⁵,   a⁴b,   a³b²,   a²b³,   ab⁴,   b⁵

and the sixth row of the Pascal triangle is

1     5     1     0     1     0     5     1

Using these two we can write

(a + b)⁵ = a⁵ + a⁴b + a³b² + a²b³ + ab⁴ + b⁵

The Pascal triangle can be constructed using additional one, without using any multiplication or division. So without multiplication we can write down the binomial expansion for (a + b)ⁿ for any n ∈ N. The above pattern resembling a triangle, is credited in the name of the seventeenth century French Mathematician Blaise Pascal, who studied mathematical properties of this structure and used this concept effectively in Probability Theory.

Binomial Theorem for Positive Integral Index

If x and y are real numbers and n is a positive integer, then

(x + y)ⁿ = ⁿC₀xⁿ + ⁿC₁x^n-1y¹ + ⁿC₂x^n-2y² + ⁿC₃x^n-3y³.............  ...................+ ⁿC_rx^n-ry^r + ........ ⁿC_nyⁿ

where ⁿC_r = n!/[(n - r)!r!] for 0 ≤ r ≤ n.

The general term or (r + 1)^th term in the expansion is given by

T_{r + 1} = ⁿC_rx^n-ry^r

We have already learnt how to multiply a binomial by itself. Finding squares and cubes of a binomial by actual multiplication is not difficult.

But the process of finding the expansion of binomials with higher powers such as (x + a)¹⁰, (x + a)¹⁷, (x + a)²⁵ etc becomes more difficult. Hence we look for a general formula which will help us in finding the expansion of binomials with higher powers. We know that

(x + a)¹ = x + a = 1C₀x¹a⁰+ 1C₁x⁰a¹

(x + a)² = x² + 2ax + a²

= 2C₀x²a⁰ + 2C₁x¹a¹ + 2C₂x⁰a²

(x + a)³ = x³ + 3x²a + 3xa² + a³

= 3C₀x³a⁰ + 3C₁x²a¹ + 3C₂x¹a² + 3C₃x⁰a³

(x + a)⁴ = x⁴ + 4x³ + 6x²a² + 4xa³ + a⁴

= 4C₀x⁴a⁰ + 4C₁x³a¹ + 4C₂x²a² + 4C₃x¹a¹ + 4C₄x⁰a⁴

For n = 1, 2, 3, 4 the expansion of (x + a)ⁿ has been expressed in a very systematic manner in terms of combinatorial coefficients. The above expressions suggest the conjecture that (x + a)ⁿ should be expressible in the form,

(x + a)ⁿ

= ⁿC₀xⁿa⁰ + ⁿC₁x^{n - 1}a¹ + ⁿC₂x^{n - 2}a² + ….......

+ ⁿC_n-1 x¹a^n-1 + ⁿC_n x⁰aⁿ

Remarks in Binomial Theorem

1. In the above expansion the power of x will get reduced and power of a will get increased. the general term is

ⁿC_rx^n-ra^r

Since this is nothing but the (r + 1)^th term, it is denoted by T_r+1

T_{r + 1} = ⁿC_rx^n-ra^r

2. The (n + 1)^th term is T_n+1 = ⁿC_nx^n-naⁿ = ⁿC_naⁿ, the last term.

Thus there are (n + 1) terms in the expansion of (x + a)ⁿ

3. The degree of x in each term decreases while that of 'a' increases such that the sum of the powers in each term is equal to n. We can write 

4. ⁿC₀, ⁿC₁, ⁿC₂, ......., ⁿCr, ........, ⁿC_n are called binomial coefficients. They are also written as C₀, C₁ , C₂, ....…, C_n.

5. From the relation ⁿC_r = nC_n-r, we see that the coefficients of terms equidistant from the beginning and the end are equal.

Middle Term in Binomial Expansion

The number of terms in the expansion of (x + a)ⁿ depends upon the index n. The index is either even (or) odd.

Let us find the middle terms.

Case (i) : n is even 

The number of terms in the expansion is (n + 1), which is odd. Hence, there is only one middle term and it is given by T_(n/2) + 1

Case (ii) : n is odd

The number of terms in the expansion is (n + 1), which is even. Hence, there are two middle terms and they are given by T_{(n + 1)/2} and T_{(n + 3)/2}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.