BINOMIAL EXPANSION FORMULA FOR 1 PLUS X WHOLE POWER N

Here we are going to see the formula for the binomial expansion formula for 1 plus x whole power n.

(1 + x)ⁿ

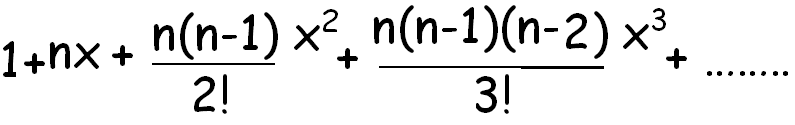
(1 - x)ⁿ

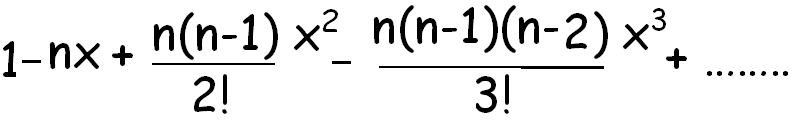
(1 + x)^-n

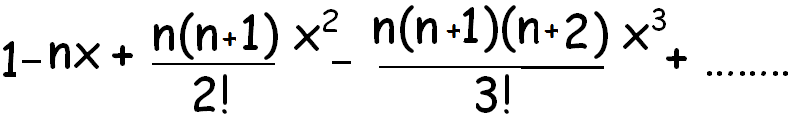
(1 - x)^-n

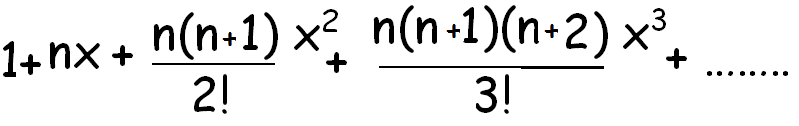
Note :

When we have negative signs for either power or in the middle, we have negative signs for alternative terms.

If we have negative for power, then the formula will change from (n - 1) to (n + 1) and (n - 2) to (n + 2).

If we have negative signs for both middle term and power, we will have a positive sign for every term.

Example 1 :

Write the first four terms in the expansion of (1 + 4x)^-5  where |x| < 1/4

Solution :

| 4x | = 4 | x | < 4 (1/4)  =  1      4x | < 1

(1 + 4x)^{− 5} can be expanded by Binomial theorem.

x = 4x , n = 5

  =  1 - 5 (4x) + (5 (5+1)/2!) (4x)²

         - (5 (5+1) (5+2)/3!) (4x)³ + .........

  =  1 - 20x + 15 (16x²) - 35 (64x³) + .........

  =  1 - 20x + 240x² - 2240x³ + .........

Example 2 :

Write the first four terms in the expansion of (1 - x²)^-4  where |x| < 1

Solution :

 (1 - x²)^-4  can be expanded by binomial theorem since

|x²| < 1 

  =  1 + 4 (x²) + (4 (4+1) /2!)(x²)²+ (4 (4+1) (4+2)/3!)(x²)³+ ...........

  =  1 + 4 (x²) + (4x5/2!)x⁴+ (4x5x6/3!)x⁶+ ...........

  =  1 + 4 x² + 10 x⁴+ 20 x⁶+ ...........

Example 3 :

Write the first four terms in the expansion of (1 - x²)^-4  where |x| < 1

Solution :

 (1 - x²)^-4  can be expanded by binomial theorem since

|x²| < 1 

  =  1 + 4 (x²) + (4 (4+1) /2!)(x²)²+ (4 (4+1) (4+2)/3!)(x²)³+ ...........

  =  1 + 4 (x²) + (4x5/2!)x⁴+ (4x5x6/3!)x⁶+ ...........

  =  1 + 4 x² + 10 x⁴+ 20 x⁶+ ...........

Example 4 :

Find the expansion of 1/(2 + x)⁴ where |x| < 2 upto the fourth term.

Solution :

1/(2 + x)⁴  =  (2 + x)^-4 = 2^-4 (1 + x/2)^-4 can be expanded by binomial theorem since

|x/2| < 1 

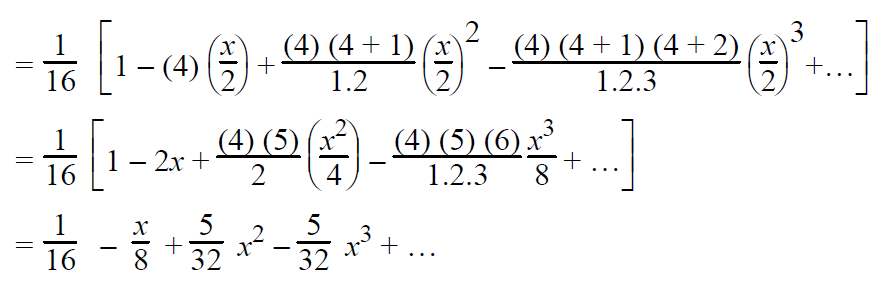
Example 5 :

Find the value of ∛126 correct to two decimal places.

Solution :

 ∛126 = (126)^1/3

   =  (125 + 1)^1/3 

   =  [125 (1 + (1/125))]^1/3

   =  125^1/3(1 + (1/125))^1/3           1/125 < 1

   = 5 [1 + (1/3)(1/125) + ..........]

   = 5 [1 + (1/3)(0.008)]

   = 5 [1 + 0.002666]

= 5.01 (correct to 2 decimal places)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.