BAYES THEOREM PRACTICE PROBLEMS

If A₁, A₂, A₃, .............A_n are mutually exclusive and exhaustive events such that P(Ai) > 0, i = 1,2,3,….n and B is any event in which P(B) > 0, then 

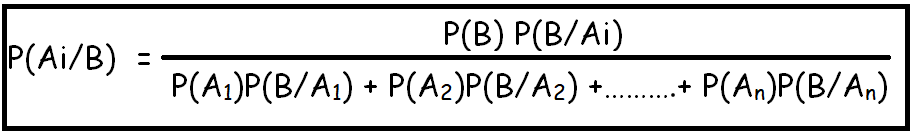
Question 1 :

A factory has two Machines-I and II. Machine-I produces 60% of items and Machine-II produces 40% of the items of the total output. Further 2% of the items produced by Machine-I are defective whereas 4% produced by Machine-II are defective. If an item is drawn at random what is the probability that it is defective?

Solution :

Probability of items produced by Machine 1

P(M₁)  =  60/100

Probability of defective items produced by Machine 1

P(D/M₁)  =  2/100

Probability of items produced by Machine 2

P(M₂)  =  40/100

Probability of defective items produced by Machine 2

P(D/M₂)  =  4/100

We need to find that if an item is drawn at random what is the probability that it is defective?

Randomly selected item will be defective either by machine 1 or machine 2.

P(D)  =  P(M₁) ⋅ P(D/M₁) +  P(M₂) ⋅ P(D/M₂)

  =  (60/100) (2/100) + (40/100) (4/100)

  =  120/10000 + 160/10000

  =  280/10000

  =  0.0280

Question 2 :

There are two identical urns containing respectively 6 black and 4 red balls, 2 black and 2 red balls. An urn is chosen at random and a ball is drawn from it. (i) find the probability that the ball is black (ii) if the ball is black, what is the probability that it is from the first urn?

Solution :

Total number of balls in Urn 1 

  =  6 black + 4 red 

  =  10 balls

Probability of getting black ball from Urn 1 

P(B/U₁)  =  6/10

Total number of balls in Urn 1 

  =  2 black + 2 red 

  =  4 balls

Probability of getting black ball from Urn 2 

P(B/U₂)  =  2/4

P(U₁)  =  1/2 and P(U₂)  =  1/2

(i) find the probability that the ball is black

P(B)  =  P(U₁) ⋅ (P(B/U₁) +  P(U₂) ⋅ (P(B/U₂)

  =  (1/2)  ⋅ (6/10) +  (1/2) ⋅ (2/4)

  =  3/10 + 1/4

 =  11/20

(ii) if the ball is black what is the probability that it is from the first urn?

We need to find the probability that the selected black ball is from first urn.

 =  P(U₁) ⋅ (P(B/U₁) / [P(U₁) ⋅ (P(B/U₁) +  P(U₂) ⋅ (P(B/U₂)]

  =   (1/2)  ⋅ (6/10) / [(1/2)  ⋅ (6/10) +  (1/2) ⋅ (2/4)]

  =  (6/20) / (11/20)

  =  6/11

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.