TRIGONOMETRIC RATIOS WORKSHEET
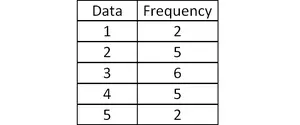
1. In the right triangle shown below, find the six trigonometric ratios of the angle θ.
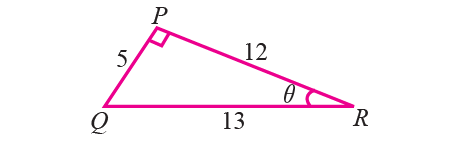
2. In the right triangle shown below, find the six trigonometric ratios of the angle θ.
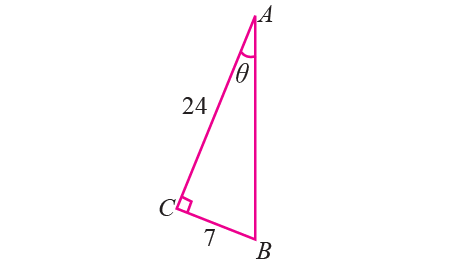
3. In triangle ABC, right angled at B, 15sinA = 12. Find the other five trigonometric ratios of the angle A. Also find the six ratios of the angle C.
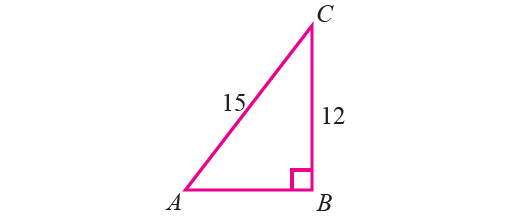
4. In the right triangle PQR shown below, find the value of sinθ and cosθ. Using them, find the value of tanθ and cotθ.

5. From the figure given below, find the value of sinθ and cosθ. Using them, find the value of tanθ and cotθ.

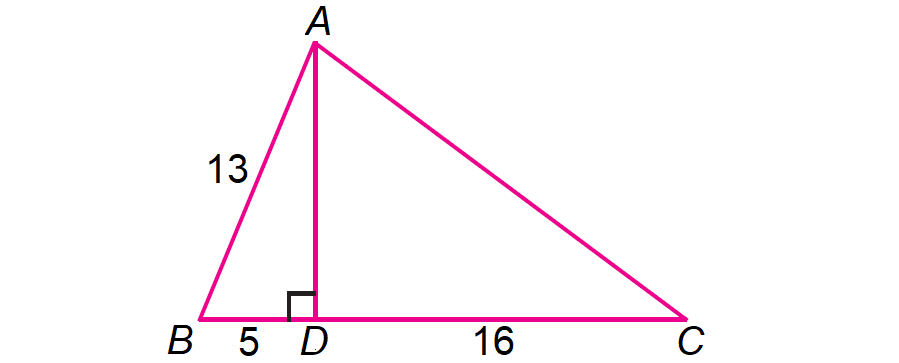
6. In the diagram below, find the values of sinB, secB, cotB, cosC, tanC and cscC.
7. If sinθ = 13/85 and cosθ = 84/85, then find the values of tanθ and cosθ.

Answers
1. Answer :

From the triangle shown above,
opposite side = 5
adjacent side = 12
hypotenuse = 13
Therefore,
sinθ = PQ/RQ = 5/13
cosθ = PR/RQ = 12/13
tanθ = PQ/PR = 5/12
cscθ = RQPQ = 13/5
secθ = RQ/PR = 13/12
cotθ = PR/PQ = 12/5
2. Answer :

From the right triangle shown above,
AC = 24
BC = 7
By Pythagorean Theorem,
AB2 = BC2 + CA2
AB2 = 72 + 242
AB2 = 49 + 576
AB2 = 625
AB2 = 252
AB = 25
Now, we can use the three sides to find the six trigonometric ratios of angle θ.
Therefore,
sinθ = BC/AB = 7/25
cosθ = AC/AB = 24/25
tanθ = BC/AC = 7/24
cscθ = AB/BC = 25/7
secθ = AB/AC = 25/24
cotθ = AC/BC = 24/7
3. Answer :
Given : 15sinA = 12.
Therefore,
opposite side = 12
hypotenuse = 15
Let us consider the right triangle ABC where right angled at B, with
BC = 12
AC = 15

By Pythagorean theorem,
AC2 = AB2 + BC2
152 = AB2 + 122
225 = AB2 + 144
225 - 144 = AB2
81 = AB2
92 = AB2
9 = AB
Now, we can use the three sides to find the five trigonometric ratios of angle A and six trigonometric ratios of angle C.
Therefore,
cosA = AB/AC = 9/15 = 3/5
tanA = BC/AB = 12/9 = 4/3
cscA = AC/BC = 15/12 = 5/4
secA = AC/AB = 15/9 = 5/3
cotA = AB/BC = 9/12 = 3/4
sinC = AB/AC = 9/15 = 3/5
cosC = BC/AC = 12/15 = 4/5
tanC = AB/BC = 9/12 = 3/4
cscC = AC/AB = 15/9 = 5/3
secC = AC/BC = 15/12 = 5/4
cotC = BC/AB = 12/9 = 4/3
4. Answer :

From the right triangle shown above,
opposite side = 5
adjacent side = 12
hypotenuse = 13
Therefore,
sinθ = PQ/RQ = 5/13
cosθ = PR/RQ = 12/13
tanθ = sinθ/cosθ = 5/13 ÷ 12/13
tanθ = 5/13 ⋅ 13/12
tanθ = 5/12
cotθ = cosθ/sinθ = 12/13 ÷ 5/13
cotθ = 12/13 ⋅ 13/5
cotθ = 12/5
5. Answer :

From the figure given above, AC = 24 and BC = 7.
By Pythagorean theorem,
AB2 = BC2 + CA2
AB2 = 72 + 242
AB2 = 49 + 576
AB2 = 49 + 576
AB2 = 625
AB2 = 252
AB = 25
Now, we can use the three sides to find the six trigonometric ratios of angle θ.
Therefore,
opposite side = 7
adjacent side = 24
hypotenuse = 25
Therefore,
sinθ = BC/AB = 7/25
cosθ = AC/AB = 24/25
tanθ = sinθ/cosθ = 7/25 ÷ 24/25
tanθ = 7/25 ⋅ 25/24
tanθ = 7/24
sinθ = BC/AB = 7/25
cosθ = AC/AB = 24/25
cotθ = cosθ/sinθ = 24/25 ÷ 7/25
cotθ = 24/25 ⋅ 25/7
cotθ = 24/7
6. Answer :

In the right ΔABD, by Pythagorean Theorem,
AB2 = AD2 + BD2
132 = AD2 + 52
169 = AD2 + 25
Subtract 25 from each side.
144 = AD2
122 = AD2
12 = AD
In the right ΔACD, by Pythagorean Theorem,
AC2 = AD2 + CD2
AC2 = 122 + 162
AC2 = 144 + 256
AC2 = 400
AC2 = 202
AC = 20
Then,
sinB = opposite side/hypotenuse = AD/AB = 12/13
secB = hypotenuse/adjacent side = AB/BD = 13/5
cotB = adjacent side/opposite side = BD/AD = 5/12
cosC = adjacent side/hypotenuse
= CD/AC
= 16/20
= 4/5
tanC = opposite side/adjacent side
= AD/CD
= 12/16
= 3/4
cscC = hypotenuse/opposite side
= AC/AD
= 20/12
= 5/3
7. Answer :
Value of tanθ :
tanθ = sinθ/cosθ
= (13/85)/(84/85)
= (13/85) ⋅ (85/84)
= (13 ⋅ 85)/(85 ⋅ 84)
= 13/84
Value of cotθ :
cotθ = 84/13
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 32)
Oct 30, 25 08:57 AM
10 Hard SAT Math Questions (Part - 32) -
10 Hard SAT Math Questions (Part - 31)
Oct 27, 25 10:32 AM
10 Hard SAT Math Questions (Part - 31) -
Time and Work Problems
Oct 20, 25 07:13 AM
Time and Work Problems - Concept - Solved Problems