BASIC TRIGONOMETRIC IDENTITIES

A trigonometric identity represents a relationship that is always true for all admissible values in the domain.

For example, 

sec θ  =  1 / cos θ

is is true for all admissible values of θ. Hence, this is an identity. 

However,

sin θ  =  1/2

is not an identity, because the relation fails when θ = 60°.

Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry which are being used in solving trigonometric equations.

The most important part of working with identities, is to manipulate them with the help of a variety of techniques from algebra.

Let us recall the fundamental identities (Pythagorean identities) of trigonometry, namely,

sin²θ + cos²θ  =  1

sec²θ - tan²θ  =  1

csc²θ - cot²θ  =  1

Points to Remember

1. sin²θ is the commonly used notation for (sin θ)², likewise for other trigonometric ratios.

2. sec²θ - tan²θ  =  1 is meaningless when θ  =  90°. But still it is an identity and true for all values of θ for which sec θ and tan θ are defined. Thus, an identity is an equation that is true for all values of its domain values.

3. When we write

sin θ / (1 + cos θ),

we understand that the expression is valid for all values of θ for which (1 + cos θ)  ≠  0

Solved Problems

Problem 1 :

Prove that 

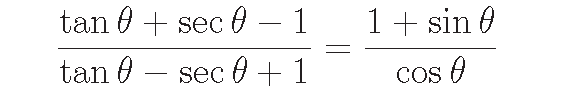
Solution :

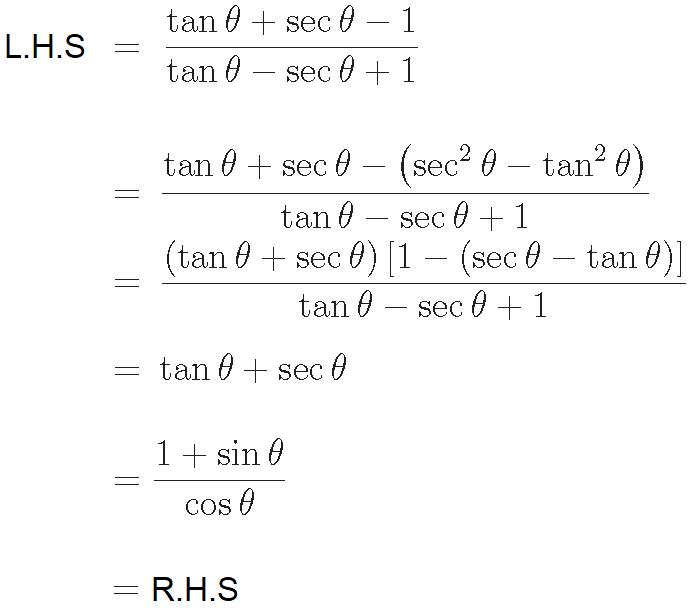
Problem 2 :

Prove that 

(secA − cosecA) (1 + tanA + cotA) = tanAsecA − cotA cosecA

Solution :

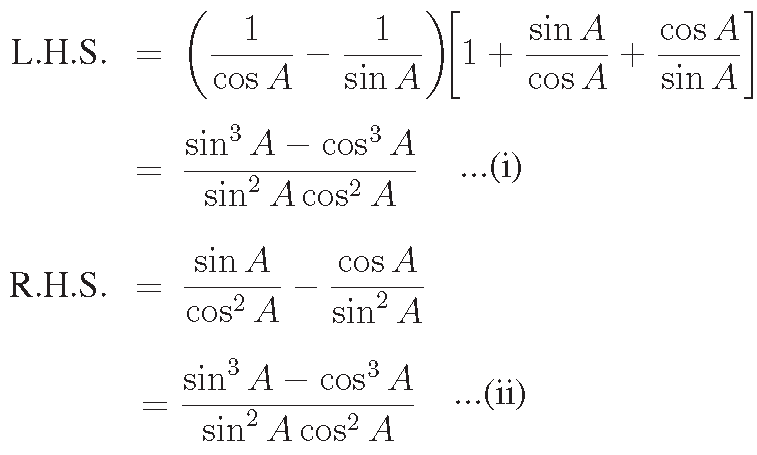
From (i) and (ii), we get the required result.

Problem 3 : 

Eliminate θ from

a cos θ  =  b

c sin θ  =  d

where a, b, c, d are constants.

Solution :

a cos θ  =  b

Multiply each side by c. 

ac cos θ  =  bc

Square each side. 

(ac cos θ)²  =  (bc)²

a²c² cos²θ  =  b²c² -----(1)

c sin θ  =  d

Multiply each side by a. 

ac sin θ  =  ad

Square each side. 

(ac sin θ)²  =  (ad)²

a²c² sin²θ  =  a²d² -----(2)

Add (1) and (2). 

a²c² cos²θ + a²c² sin²θ  =  b²c²  +  a²d²

a²c²(cos²θ + sin²θ)  =  b²c²  +  a²d²

a²c²(1)  =  b²c²  +  a²d²

a²c²  =  b²c²  +  a²d²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.