BASIC MATH RULES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Addition Rules
Rule 1 :
Positive + Positive = Add
The result will be positive
Example :
2 + 1 = 3
Rule 2 :
Negative + Negative = Add
The result will be negative
Example :
-3 + (-5) = -8
Subtraction Rules
Rule 1 :
Negative + Positive = Subtract
Take sign of number with largest absolute value
Example :
-3 + 5 = 2
Rule 2 :
Positive + Negative = Subtract
Take sign of number with largest absolute value
Example :
3 + (-5) = -2
Multiplication Rules
Rule 1 :
Positive x Positive = Positive
Example :
3 x 5 = 15
Rule 2 :
Negative x Negative = Positive
Example :
(-3) x (-5) = 15
Rule 2 :
Positive x Negative = Negative
Example :
3 x (-5) = -15
Rule 2 :
Negative x Positive = Negative
Example :
-3 x 5 = -15
Division Rules
Rule 1 :
Positive ÷ Positive = Positive
Example :
20 ÷ 4 = 5
Rule 2 :
Negative ÷ Negative = Positive
Example :
(-20) ÷ (-4) = 5
Rule 2 :
Positive ÷ Negative = Negative
Example :
20 ÷ (-4) = -5
Rule 2 :
Negative ÷ Positive = Negative
Example :
-20 ÷ 4 = -5
Exponent Rules
Rule 1 :
xm ⋅ xn = xm+n
Example :
34 ⋅ 35 = 34+5
34 ⋅ 35 = 39
Rule 2 :
xm ÷ xn = xm-n
Example :
37 ÷ 35 = 37-5
37 ÷ 35 = 32
Rule 3 :
(xm)n = xmn
Example :
(32)4 = 3(2)(4)
(32)4 = 38
Rule 4 :
(xy)m = xm ⋅ ym
Example :
(3 ⋅ 5)2 = 32 ⋅ 52
(3 ⋅ 5)2 = 9 ⋅ 25
(3 ⋅ 5)2 = 225.
Rule 5 :
(x/y)m = xm/ym
Example :
(3/5)2 = 32/52
(3/5)2 = 9/25
Rule 6 :
x-m = 1/xm
Example :
3-2 = 1/32
3-2 = 1/9
Rule 7 :
x0 = 1
Example :
30 = 1
Rule 8 :
x1 = x
Example :
31 = 3
Rule 9 :
xm/n = y ----> x = yn/m
Example :
x1/2 = 3
x = 32/1
x = 32
x = 9
Rule 10 :
(x/y)-m = (y/x)m
Example :
(5/3)-2 = (3/5)2
(5/3)-2 = 32/52
(5/3)-2 = 9/25
Rule 11 :
ax = ay ----> x = y
Example :
3m = 35 ----> m = 5
Rule 12 :
xa = ya ----> x = y
Example :
k3 = 53 ----> k = 5
Order of Operations (PEMDAS)
This rule can be used to simplify or evaluate complicated numerical expressions with more than one binary operation easily.
Very simply way to remember PEMDAS rule :
P ----> Parenthesis
E ----> Exponents
M ----> Multiplication
D ----> Division
A ----> Addition
S ----> Subtraction
Important notes :
1. In a particular simplification, if you have both multiplication and division, do the operations one by one in the order from left to right.
2. Multiplication does not always come before division. We have to do one by one in the order from left to right.
3. In a particular simplification, if you have both addition and subtraction, do the operations one by one in the order from left to right.
Examples :
15 ÷ 3 x 2 = 5 x 2 = 10
24 - 8 + 5 = 16 + 5 = 21
In the above simplification, we have both division and multiplication. From left to right, we have division first and multiplication next.
So we do division first and multiplication next.
For more examples on PEMDAS, click here
Percent Equation
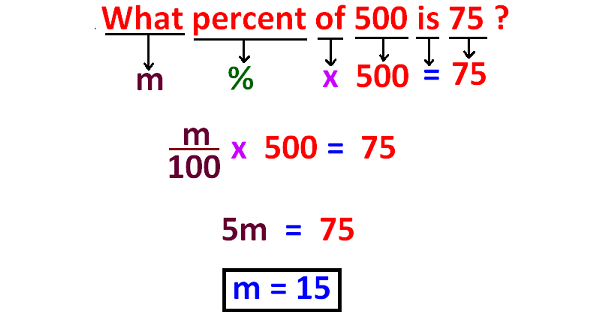
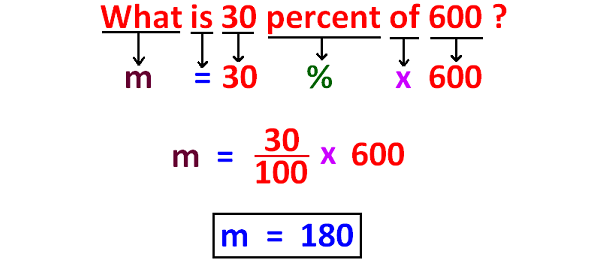
Percent Decrease / Increase
The formula given below can be used to find the percent increase or decrease of a value.
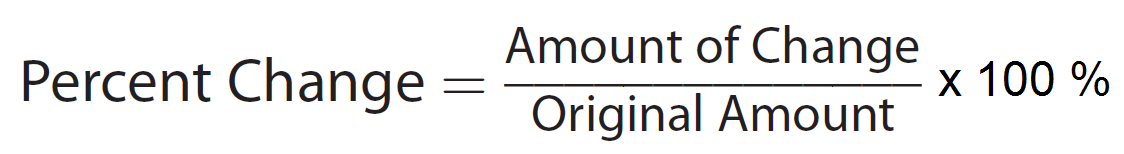
The change may be an increase or a decrease.
Here, the original amount is the value before increase or decrease.
For more examples on percent increase/decrease,
Place Value

Place value of a digit in a number is the digit multiplied by thousand or hundred or whatever place it is situated.
Example :
In 25486, the place value of 5 is
= 5 ⋅ 1000
= 5000
Here, to get the place value of 5, we multiply 5 by 1000.
Because 5 is at thousands place.
Face Value
Face value of a digit in a number is the digit itself.
More clearly, face value of a digit always remains same irrespective of the position where it is located.
Example :
In 25486, the face value of 5 is 5.
The difference between place value and face value
The difference between place value and face has been illustrated in the picture shown below.
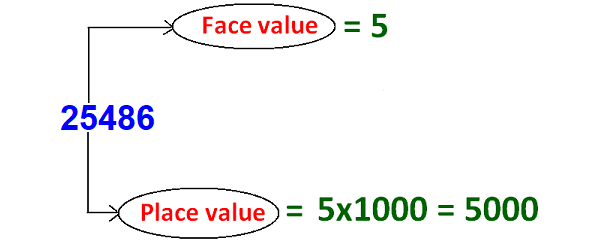
Angles
Acute Angle : Less than 90°
Obtuse Angle : More than 90°
Right Angle : 90°
Straight Angle : 180°
Complementary Angles :
Two angles the sum of whose measures is 90 degrees.
Supplementary Angles :
Two angles the sum of whose measures is 180 degrees.
Triangles
Triangles :
1. The sum of the lengths of any two sides of a triangle is greater than the third side.
2. The sum of all the three angles of a triangle is 180°.
Isosceles Triangle :
Two sides equal ; two equal angles
Equilateral Triangle :
Three sides equal ; three equal angles
Right Triangles :
Pythagorean Theorem :
a2 + b2 = c2
where a and b are the measures of the legs of the triangle and c is the hypotenuse.
Statistics
Mean (Average) :
Sum of all values divided by number of values.
Median :
Middle value when the values are arranged numerically.
Mode :
The data value that occurs most frequently.
Probability
Probability of the event A :
P(A) = The frequency of A/Total sample size
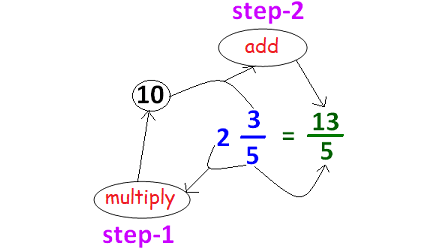
Converting Mixed Number to Improper fraction
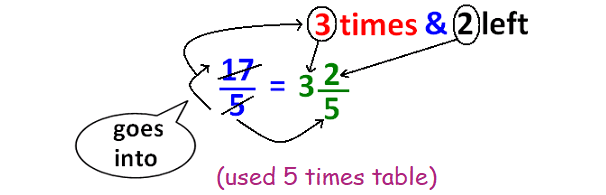
Converting Improper fraction to Mixed Number
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

