ARITHMETIC PRACTICE PROBLEMS WITH SOLUTIONS

Question 1 :

If u^-4  =  16, what is one possible value of u ?

(A) 4       (B) 2       (C) 1       (D) 1/2       (E) 1/4

Answer :

u^-4  =  16

u  =  16^-1/4

=  (1/16)^1/4

=  1/(16)^1/4

=  1/(2⁴)^1/4

=  1/2

Question 2 :

If a kilogram is equal to approximately 2.2 pounds, which of the following is the best approximation of the number of kilograms in one pound ?

(A) 11/5     (B) 5/8     (C) 5/11     (D) 1/3     (E) 1/5

Answer :

To get rid of decimals in a fraction, multiply the top and bottom by the smaller power of 10 we can.

If you need to move a decimal over 2 places, multiply the top and bottom by 100.

1 kilogram/2.2 pounds  =  x kilograms/1 pound

x  =  1/2.2

=  10/22

=  5/11

Question 3 :

If r is positive, and p is negative, which of the following must be negative ?

(A) rp + 2     (B) -|rp|     (C) r²p² - 10

(D) -(r + p)²     (E) (r + p)³

Answer :

Let us take option B, -|rp|

By multiplying positive and negative number, we get negative number. But the negative is in absolute sign, the answer will be positive.

In front of |rp|, we have negative sign. So the final answer will always be negative.

Question 4 :

If a is a positive integer, then what is the value of 5^a + 5^{a + 1} ?

(A) 6^a    (B) 5^a - 1    (C) 5^2a + 1    (D) (5^a)^a - 1    (E)  6(5^a)

Answer :

  =  5^a + 5^{a + 1}

  =  5^a + 5^a ⋅ 5

  =  5^a(1 + 5)

  =  5^a ⋅ 6

  =  6⋅5^a

Question 5 :

X, Y and Z are points on a line in that order. XY is 20, and YZ is 15 more than XY. What is XZ ?

(A) 25       (B) 35       (C) 45       (D) 55       (E) 65

Answer :

XY  =  20

YZ  =  15 + 20  =  35

From this, we come to know that Y lies between X and Z

XZ  =  XY + YZ

  =  20 + 35

  =  55

Question 6 :

The sum of the ages of 3 people A, B and C is 90 years. What would be the total of their ages 4 years back?

a) 74 years       b) 78 years       c) 86 years      d) 80 years

Answer :

Sum of ages of three people A, B and C = 90

A + B + C = 90

Age of A four years back = A - 4

Age of B four years back = B - 4

Age of C four years back = C - 4

= A - 4 + B - 4 + C - 4

= (A + B + C) - 12

= 90 - 12

= 78

So, option b is correct.

Question 7 :

A circle has a radius of 6 cm. What would be the area of an inscribed equilateral triangle?

Answer :

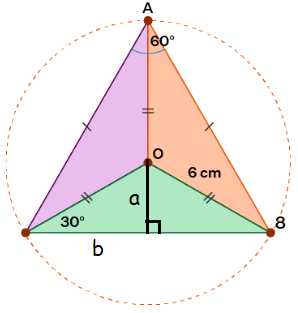
In special right triangle, 

Hypotenuse = 6 cm = radius

Smaller side = a, longer side = a√3

a² + b² = 6²

a² + (a√3)² = 6²

a² + 3a² = 6²

4a² = 36

a² = 36/4

a² = 9

a = 3

b = a√3 = 3√3

2b = 6√3

Now the area of the equilateral triangle is

= √3/4 × (side)²

Area = √3 / 4 × 6√3 × 6√3

Area = 27√3 cm²

Question 8 :

‘A’ sells a DVD to ‘B’ at a gain of 17% and ‘B’ then sells it to ‘C’ at a loss of 25%. If 'C' pays $1053 to ‘B’. then what is the cost price of the DVD to ‘A’ ?

a)  1200   b)  1450      c)  1250     d)  1375

Answer :

B is selling the DVD at the loss of 25%

75% of B = 1053

0.75(B) = 1053

B = 1053/0.75

B = 1404

A is selling DVD at the profit of 17%

117% of A = 1404

1.17A = 1404

A = 1200

So, option a is correct.

Question 9 :

How many strings of 5 digits have the property that the sum of their digits is 7?

a)  66        b)  330       c)  495      d)  99

Answer :

Sum of the digits to be chosen = 7

Possible digits are 0, 1, 2, 3, 4, 5, 6 and 7

Partition of 7 :

7, 0, 0, 0, 0

6, 1, 0, 0, 0

5, 2, 0, 0, 0

5, 1, 1, 0, 0

4, 3, 0, 0, 0

4, 2, 1, 0, 0

4, 1, 1, 1, 0

3, 3, 1, 0, 0

3, 2, 2, 0, 0

3, 2, 1, 1, 0

3, 1, 1, 1, 1

2, 2, 2, 1, 0

2, 2, 1, 1, 1

Arrangement of above Parition

= 5!/4! + 5!/3! + 5!/3! + 5!/2!2! + 5!/3! + 5!/2! + 5!/3! + 5!/2!2! + 5!/2!2! + 5!/2! + 5!/4! + 5!/3! + 5!/3!2!

= 5 + 20 + 20 + 30 + 20 + 60 + 20 + 30 + 30 + 60 + 5 + 20 + 10

= 330

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.