ARGUMENT OF A COMPLEX NUMBER IN DIFFERENT QUADRANTS

Let (r, θ) be the polar co-ordinates of the point.

P = P(x, y) in the complex plane corresponding to the complex number

z = x + iy

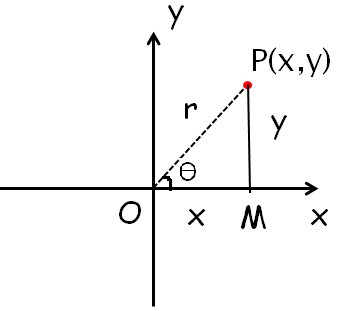
cos θ = Adjacent side/hypotenuse side ==> OM/MP ==> x/r

sin θ = Opposite side/hypotenuse side ==> PM/OP ==> y/r

x = r cos θ and y = r sin θ

tan θ  = y/x

θ = tan⁻¹ y/x 

is called the amplitude or argument of z = x + iy

denoted by amp z or arg z and is measured as the angle which the line OP makes with the positive x-axis (in the anti clockwise sense).

How to find argument of complex number ?

Usually we have two methods to find the argument of a complex number

(i) Using the formula θ = tan⁻¹ y/x  

here x and y are real and imaginary part of the complex number respectively.

This formula is applicable only if x and y are positive.

But the following method is used to find the argument of any complex number.  

Argument of a complex number in different quadrants

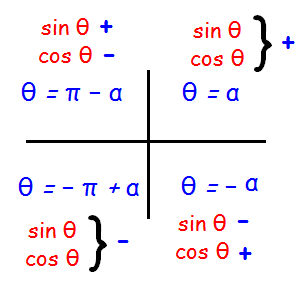
To find the modulus and argument for any complex number we have to equate them to the polar form

r (cos θ + i sin θ)

Here r stands for modulus and θ stands for argument

Let us see some example problems to understand how to find the modulus and argument of a complex number.

Example 1 :

Find the modulus and argument of the complex number

- √2 + i √2

Solution :

- √2 + i √2 = r (cos θ  + i sin θ) ----(1)

r = √ [(-√2)² + √2²] = √(2 + 2) = √4 = 2

r = 2

Apply the value of r in the first equation

- √2 + i √2 = 2 (cos θ  + i sin θ)

- √2 + i √2 = 2 cos θ  + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ is positive and cos θ is negative the required and θ lies in the second quadrant.

θ = Π - α

Here α is nothing but the angles of sin and cos for which we get the value 1/√2

θ = Π - (Π/4)

θ = (4Π-Π)/4 ==> 3Π/4

Modulus = 2 and argument = 3Π/4

Hence - √2 + i √2 = 2 (cos 3Π/4  + i sin 3Π/4)

Example 2 :

Find the modulus and argument of a complex number

1 + i √3

Solution :

1 + i √3 = r (cos θ  + i sin θ) ----(1)

r = √ [(1)² + √3²] = √(1 + 3) = √4 = 2

r = 2

Apply the value of r in the first equation

1 + i √3 =  2 (cos θ  + i sin θ)

1 + i √3 = 2 cos θ  + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ and cos θ are positive, the required and θ lies in the first quadrant.

θ = α

Here α is nothing but the angles of sin and cos for which we get the values 1/2 and √3/2 respectively.

θ = Π/3

Modulus = 2 and argument = Π/3

Hence - √2 + i √2 = 2 (cos Π/3  + i sin Π/3)

Example 3 :

Find the modulus and argument of the complex number

-1 - i √3

Solution :

-1 - i √3 = r (cos θ  + i sin θ) ----(1)

r = √ [(-1)² + (-√3)²] = √(1 + 3) = √4 = 2

r = 2

Apply the value of r in the first equation

-1 - i √3 =  2 (cos θ  + i sin θ)

-1 - i √3 = 2 cos θ  + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ and cos θ are negative the required and θ lies in the third quadrant.

θ = -Π + α

Here α is nothing but the angles of sin and cos for which we get the values √3/2 and 1/2 respectively.

θ  =  - Π + α

     =  - Π + Π/3 ==> (-3Π+Π)/3 ==>  -2Π/3

Modulus = 2 and argument  =  -2Π/3

Hence - 1 - i √3 = 2 (cos (-2Π/3)  + i sin (-2Π/3))

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.