AREAS OF CIRCLES AND SECTORS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Area of a Circle
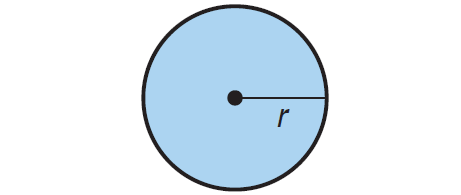
The area of a circle is π times the square of the radius.
A = πr2
Area of a Sector
The sector is the region bounded by two radii of the circle and their intercepted arc. In the diagram shown below, sector APB is bounded by radii AP, BP and arc arc AB.
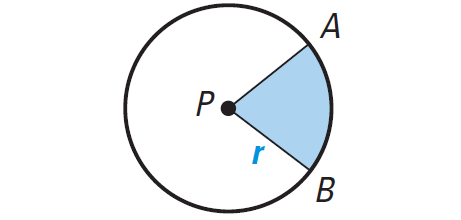
The ratio of the area A of a sector of a circle to the area of the circle is equal to the ratio of the measure of the intercepted arc to 360°.
A/πr2 = m∠arc AB/360°
So, the area of the sector is
A = [m∠arc AB / 360°] ⋅ πr2
Finding the Area of a Circle
Example 1 :
Find the area of the circle shown below.
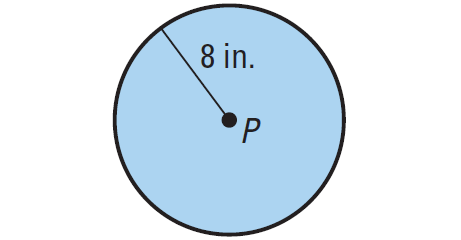
Solution :
Formula area of a circle is given by
A = πr2
Substitute r = 8.
A = π(8)2
A = 64π
Use calculator.
A ≈ 201.06
So, the area is 64π, or about 201.06, square inches.
Using the Area of a Circle
Example 2 :
If the area of a circle is 96 square centimeters, find its diameter.
Solution :
Formula area of a circle is given by
A = πr2
Substitute A = 96.
96 = πr2
Divide each side π.
96/π = πr2/π
96/π = r2
Use calculator.
30.56 ≈ r2
Take square root on each side.
5.53 ≈ r
So, the diameter of the circle is about 2(5.53), or about 11.06, centimeters.
Finding the Area of a Sector
Example 3 :
Find the area of the sector shown at the right.
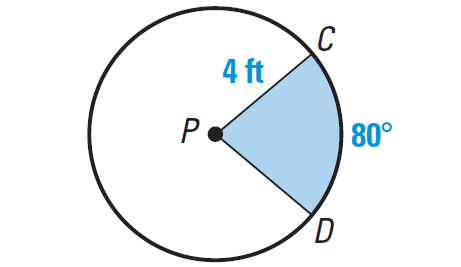
Solution :
Sector CPD intercepts an arc whose measure is 80°. The radius is 4 feet.
Formula for area of a sector is given by
A = [m∠arc CD/360°] ⋅ πr2
Substitute m∠arc CD = 80° and r = 4.
A = [80°/360°] ⋅ π(4)2
A = (2/9) ⋅ 16π
Use calculator.
A ≈ 11.17
So, the area of the sector is about 11.17 square feet.
Example 4 :
A and B are two points on a ⊙P with radius 9 inches and ∠APB = 60°. Find the areas of the sectors formed by ∠APB.
Solution :
Draw a diagram of ⊙P and ∠APB. Shade the sectors. Label a point Q on the major arc.
Find the measures of the minor and major arcs.
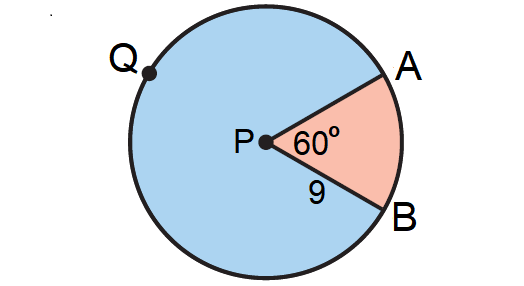
Because m∠APB = 60°, we have
m∠arc AB = 60°
and
m∠AQB = 360° - 60° = 300°
Use the formula for the area of a sector.
A = [m∠arc CD/360°] ⋅ πr2
Substitute m∠arc CD = 80° and r = 4.
A = [80°/360°] ⋅ π(4)2
A = (2/9) ⋅ 16π
Use calculator.
A ≈ 11.17
So, the area of the sector is about 11.17 square feet.
|
Area of Smaller Sector A = 60°/360° ⋅ π(9)2 A = 1/6 ⋅ π ⋅ 81 A ≈ 42.41 square inches |
Area of Larger Sector A = 300°/360° ⋅ π(9)2 A = 5/6 ⋅ π ⋅ 81 A ≈ 212.06 square inches |
Finding the Area of a Region
We may need to divide a figure into different regions to find its area. The regions may be polygons, circles, or sectors. To find the area of the entire figure, add or subtract the areas of the separate regions as appropriate.
Example 5 :
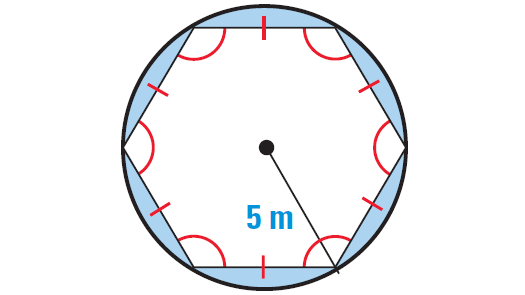
Find the area of the shaded region shown below.
Solution :
The diagram shows a regular hexagon inscribed in a circle with radius 5 meters. The shaded region is the part of the circle that is outside of the hexagon.
Area of shaded region = Area of circle - Area of hexagon
Area of shaded region = πr2 - 1/2 ⋅ a ⋅ p
Radius of the circle is 5 and the apothem of a hexagon is
= 1/2 ⋅ side length ⋅ √3
= 1/2 ⋅ 5 ⋅ √3
= 5√3/2
So, the area of the shaded region is
= [π ⋅ 52] - [1/2 ⋅ (5√3/2) ⋅ (6 ⋅ 5)]
= 25π - 75√3/2
Use calculator.
≈ 13.59
So, the area of the shaded region is about 13.59 square meters.
Example 6 :
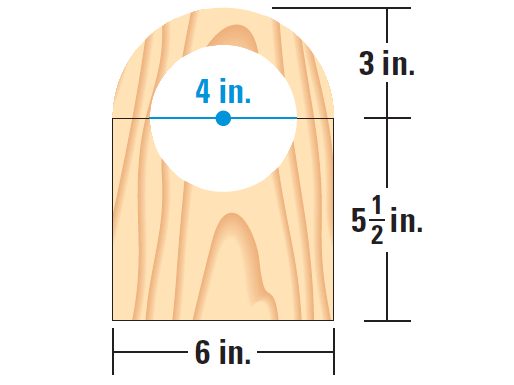
You are cutting the front face of a clock out of wood, as shown in the diagram. What is the area of the front of the case ?
Solution :
The front of the case is formed by a rectangle and a sector, with a circle removed. Note that the intercepted arc of the sector is a semicircle.
So, the required area is
= Area of rectangle + Area of sector - Area of circle
= [6 ⋅ 11/2] + [180°/360° ⋅ π ⋅ 32] - [π ⋅ (1/2 ⋅ 4)2]
= 33 + 9/2 ⋅ π - 4π
Use calculator.
≈ 34.57
The area of the front of the case is about 34.57 square inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
US Common Core K-12 Curriculum Algebra Word Problems
Dec 20, 25 01:19 AM
US Common Core K-12 Curriculum Algebra Word Problems on Systems of LInear Equations -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Dec 20, 25 01:18 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
10 Hard SAT Math Questions (Part - 40)
Dec 18, 25 06:27 PM
10 Hard SAT Math Questions (Part - 40)
