AREA OF RECTANGLE
A rectangle is a four-sided polygon where the lengths of opposite sides will be equal and each vertex angle will be 90° or right angle as shown below.
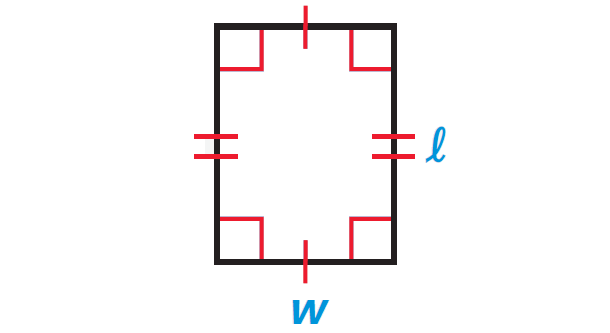
To get the area of any rectangle, we have to multiply its length and width.
Let l be the length and w be the width of a rectangle.
Then, the formula for area of the rectangle :
= l ⋅ w
Example 1 :
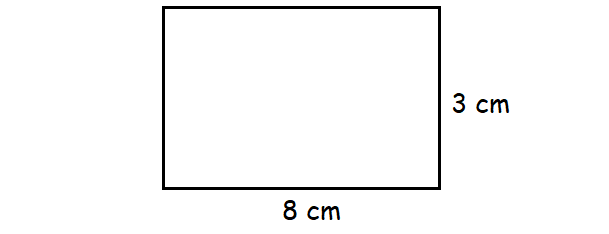
Find the area of the rectangle figure shown below.
Solution :
The figure shown above is a rectangle with 3 cm length and 8 cm width.
Formula for area of a rectangle :
= l ⋅ w
Substitute 3 for l and 8 for w.
= 3 ⋅ 8
= 24 cm2
Example 2 :
Find the area of a rectangle, if its length is 15 cm and width is 20 cm.
Solution :
Formula for area of a rectangle :
= l ⋅ w
Substitute 15 for l and 20 for w.
= 15 ⋅ 20
= 300 cm2
Example 3 :
The length of a rectangle is 3 times its width. If its perimeter is 32 ft., then find the area of the rectangle.
Solution :
Let x be the width of the rectangle.
Then, its length is 3x.
Perimeter of the rectangle is 32 ft
2(l + w) = 32
Divide each side by 2.
l + w = 16
Substitute 3x for l and x for w.
3x + x = 16
4x = 16
Divide each side by 4.
x = 4
Therefore, width of the rectangle is 4 ft.
And length of the rectangle is
= 3(4)
= 12 ft
Formula for area of a rectangle :
= l ⋅ w
Substitute 12 for l and 4 for w.
= 12 ⋅ 4
= 48 ft2
Example 4 :
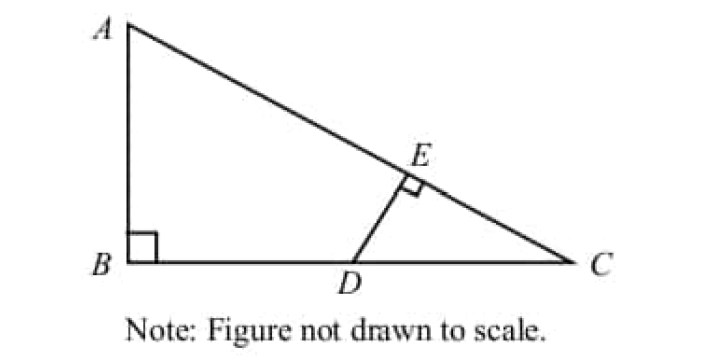
If the length of each diagonal of a rectangle is 13 cm and its width is 12 cm, then find the area of the rectangle.
Solution :
To find the area of a rectangle, we have to know its length and width. Width is given in the question, that is 12 cm. So, find its length.
Draw a sketch.
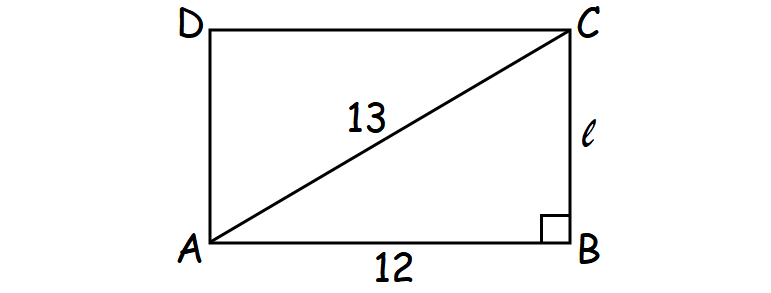
In the figure shown above, consider the right triangle ABC.
By Pythagorean Theorem, we have
AB2 + BC2 = AC2
Substitute.
122 + l2 = 132
Simplify and solve for l.
144 + l2 = 169
Subtract 144 from each side.
l2 = 25
Find positive square root on both sides.
√l2 = √25
l = 5
Therefore, the length of the rectangle is 5 cm.
Formula for area of a rectangle :
= l ⋅ w
Substitute 5 for l and 12 for w.
= 5 ⋅ 12
= 60 cm2
Example 5 :
The length and width of a rectangle are in the ratio 3 : 4 and its area is 588 square inches. Find its length and width.
Solution :
From the ratio 3 : 4, let the length and width of the rectangle be 3x and 4x respectively.
Area of the rectangle = 588 in2
l ⋅ w = 588
Substitute 3x for l and 4x for w.
3x ⋅ 4x = 588
12x2 = 588
Divide each side by 12.
x2 = 49
Find positive square root on both sides.
√x2 = √49
x = 7
Length = 3x = 3(7) = 21 in
Width = 4x = 4(7) = 28 in
Example 6 :
The floor of a room is in rectangular shape and it has 13 m length and 9 m width. If the cost of the carpet is $12.40 per square meter, find the total cost of carpeting the floor of the room.
Solution :
To find the total cost of carpeting the floor of the room, we have to know its area. Because the floor of the room is in rectangle shape, we can use the formula for area of a rectangle to find the area of the floor.
Formula for area of a rectangle :
= l ⋅ w
Substitute 13 for l and 9 for w.
= 13 ⋅ 9
= 117
So, the area of the floor is 117 square meters.
The cost of carpet is $12.40 per square meter.
Then, the total cost of carpet for 117 square meters :
= 117 ⋅ 12.40
= $1450.80
Example 7 :
A watercolor painting is 20 inches long by 9 inches wide. Ramon makes a border around the watercolor painting by making a mat that adds 1 inch to each side of the length and the width. What is the area of the mat ?
Solution :
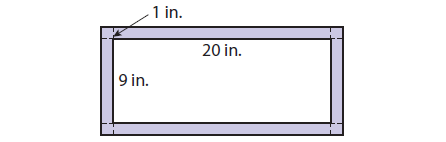
Length of the mat is
= 20 + 1 + 1
= 22 inches
Width of the mat is
= 9 + 1 + 1
= 11 inches
The area of the mat is
= Total area added - The original area of the water color
= (22 ⋅ 11) - (20 ⋅ 9)
= 242 - 180
= 62 in2
Example 8 :
Perimeter of a square and a rectangle is same. If a side of the square is 15 cm and one side of the rectangle is 18cm, find the area of the rectangle.
Solution :
Side length of square = 15 cm
Perimeter of square = 4a
= 4(15)
= 60 cm
Perimeter of square = perimeter of rectangle
2(l + w) = 60
Here length is given that 18 cm
2(18 + w) = 60
18 + w = 60/2
18 + w = 30
w = 30 - 18
w = 12 cm
Area of the rectangle = length x width
= 18 x 12
= 216 cm2
So, the required area is 216 cm2.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 217)
Jul 16, 25 07:29 AM
Digital SAT Math Problems and Solutions (Part - 217) -
Digital SAT Math Problems and Solutions (Part - 216)
Jul 16, 25 01:28 AM
Digital SAT Math Problems and Solutions (Part - 216) -
Digital SAT Math Problems and Solutions (Part - 215)
Jul 15, 25 01:24 PM
Digital SAT Math Problems and Solutions (Part - 215)