AREA OF QUADRILATERAL
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A plane figure bounded by four sides is known as a quadrilateral. The straight line joining the opposite corners is called its diagonal. The diagonal divides the quadrilateral in to two triangles.
Area of Quadrilateral General Formula
Let us derive the area of quadrilateral general formula. Consider the quadrilateral ABCD shown below :
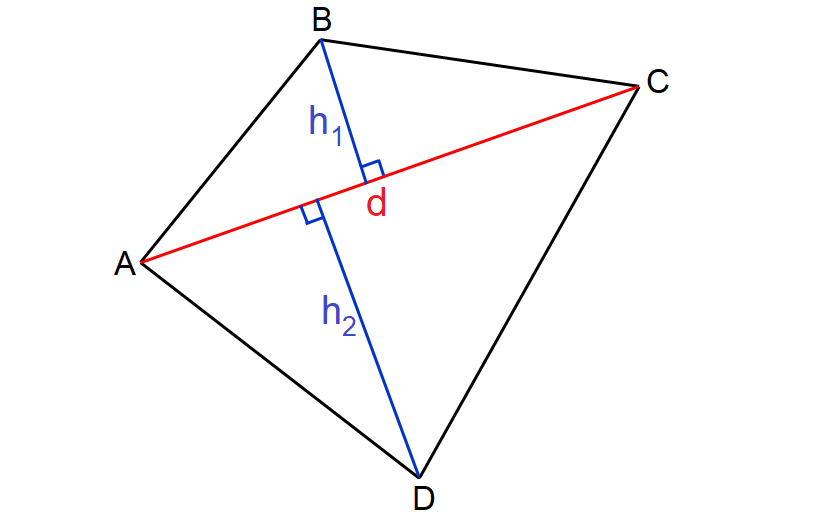
We can observe the quadrilateral above as a combination of two triangles, considering the diagonal AC (or d) as common base. h1 and h2 are the heights of the two triangles.
Area of quadrilateral ABCD above can be calculated by adding the areas of two two triangles ABC and ADC.
The area of quadrilateral ABCD is
= Area of Δ ABC + Area of Δ ADC
= 1/2 ⋅ d ⋅ h1 + 1/2 ⋅ d ⋅ h2
= = 1/2 ⋅ d ⋅ (h1 + h2)
Area of quadrilateral general formula :
= 1/2
x
length of the diagonal
x
sum of the lengths of perpendiculars drawn to the diagonal
Here is the list of the formulas to find the area of quadrilaterals such as square, rectangle, parallelogram, trapezoid, kite and rhombus.
Square
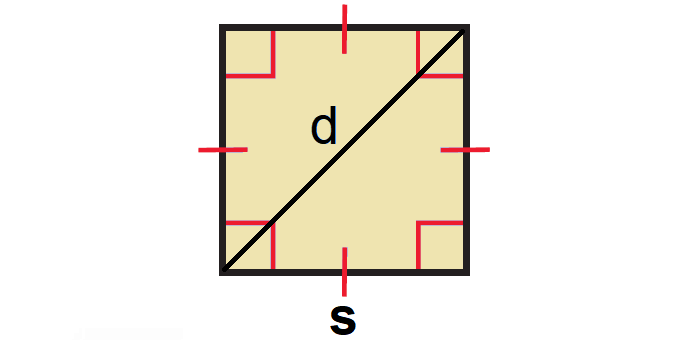
The area of a square is the product of the lengths of its two sides or square of the length of its diagonal.
Area = s ⋅ s = s2
Area = 1/2 ⋅ d2
Rectangle
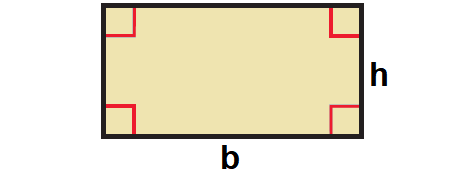
The area of a rectangle is the product of its base and height.
Area = b ⋅ h
Parallelogram
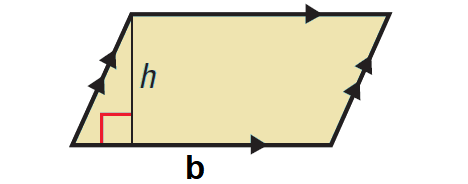
The area of a parallelogram is the product of a base and its corresponding height.
Area = b ⋅ h
Trapezoid (Trapezium)
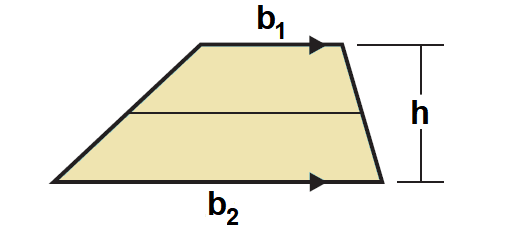
The area of a trapezoid is one half the product of the height and sum of the bases.
Area = 1/2 ⋅ h ⋅ (b1 + b2)
Kite
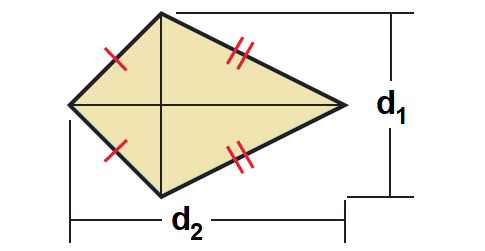
The area of a kite is one half the product of the lengths of its diagonals.
Area = 1/2 ⋅ d1 ⋅ d2
Rhombus
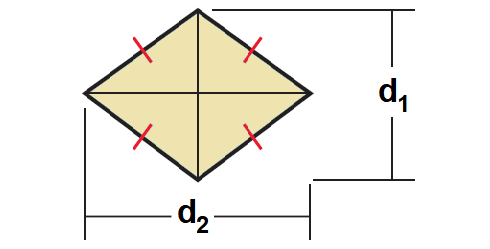
The area of a rhombus is one half the product of the lengths of its diagonals.
Area = 1/2 ⋅ d1 ⋅ d2
Problem 1 :
Find the area of parallelogram
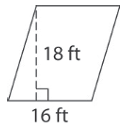
Solution :
Base = 16 ft and height = 18 ft
Area of parallelogram = base x height
= 16 x 18
= 288 square feet
Problem 2 :
Find the area of trapezium
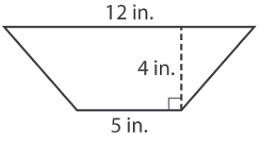
Solution :
Let the lengths of bases be a and b. Height be h.
a = 12 in, b = 5 in and h = 4 in
Area of trapezium = (1/2) x h (a + b)
= (1/2) x 4 x (12 + 5)
= 2(17)
= 34 square inches.
Problem 3 :
Find the area of rhombus.
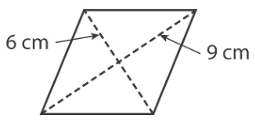
Solution :
Let d1 and d2 be the diagonals.
d1 = 9 cm and d2 = 6 cm
Area of rhombus = (1/2) x d1 x d2
= (1/2) x (9 x 6)
= 9 x 3
= 27 square cm.
Problem 4 :
A desktop in the shape of a parallelogram has a base of 30 inches and a height of 40 inches. What is the area of the desktop?
Solution :
Base = 30 in and height = 40 in
Area of parallelogram = base x height
= 30 x 40
= 1200 square inches
Problem 5 :
A rhombus has one diagonal that is 14 centimeters long and one diagonal that is 12 centimeters long. What is the area of the rhombus?
Solution :
Let d1 and d2 be the diagonals.
d1 = 14 cm and d2 = 12 cm
Area of rhombus = (1/2) x d1 x d2
= (1/2) x (14 x 12)
= 7 x 12
= 84 square cm.
Problem 6 :
The bases of a trapezoid are 24 feet and 16 feet. The height of the trapezoid is 12 feet. What is the area of the trapezoid?
Solution :
Let the lengths of bases be a and b. Height be h.
a = 24 feet, b = 16 feet in and h = 12 feet
Area of trapezium = (1/2) x h (a + b)
= (1/2) x 12 x (24 + 16)
= 6 x 40
= 240 square feet
Problem 7 :
A rectangular shaped swimming pool with dimensions 30 m × 20 m has 5 m wide cemented path along its length and 8 m wide path along its width (as shown in figure). Find the cost of cementing the path at the rate of $200 per m2.
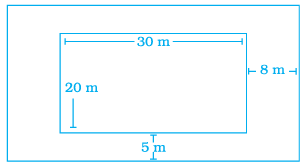
Solution :
Area of cementing path = Area of large rectangle - area of small rectangle
Length of large rectangle = 30 + 8 + 8
= 46 m
Width of the rectangle = 20 + 5 + 5
= 30 m
Area of large rectangle = 46 x 30
= 1380 m2
Area of small rectangle = 30 x 20
= 600 m2
Area of cementing path = 1380 - 600
= 780 m2
Amount to be spent = 780 x 200
= $156, 000
Problem 8 :
Find the area of the shaded portion.
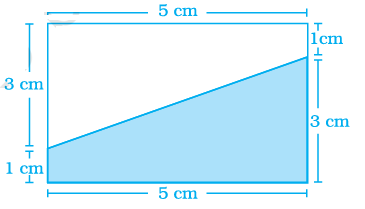
Solution :
Area of trapezium = (1/2) x height x (a + b)
height = 5 cm, a = 1 cm and b = 3 cm
= (1/2) x 5 x (1 + 3)
= (1/2) x 5 x 4
= 2 x 5
= 10 cm2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems