FINDING AREA USING INTEGRATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We can use definite integrals to find the area of a region bounded by a curve, x or y-axis and the lines. For example, consider the curve y = f(x) above the x-axis as shown below.
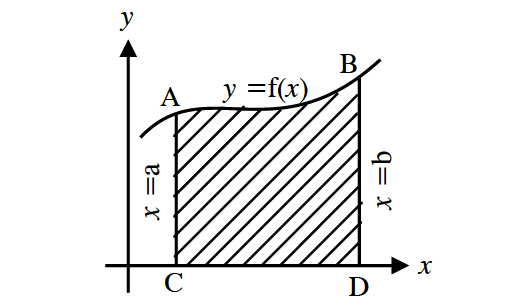
Then, the area bounded by the curve y = f(x), the x-axis and the ordinates x = a and x = b is given by
Let the curve y = f(x) be below the x-axis as shown below.
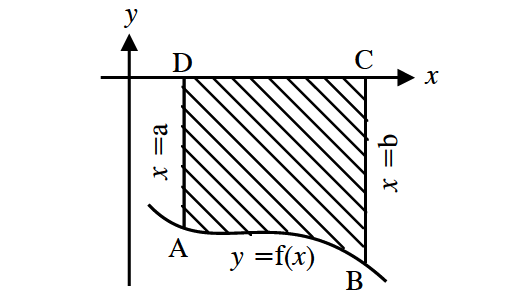
Then, the area bounded by the curve y = f(x), the x-axis and the ordinates x = a and x = b is given by
Example 1 :
Find the area of the region bounded by the line y = x - 3, x = 1, x = 5 and x-axis.
Solution :
The line y = x - 3 crosses x-axis at x = 3.
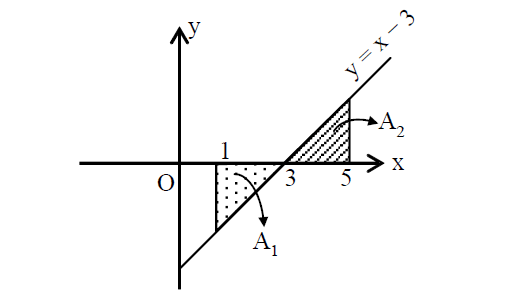
From the diagram, it is clear that A1 lies below x-axis.
Then, we have
As A2 lies above the x-axis,
Therefore, the total area is
Example 2 :
Find the area of the region bounded by y = x2 - 5x + 4, x = 2, x = 3 and x-axis.
Solution :
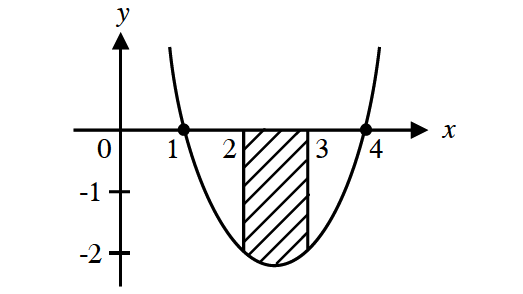
Required area is
Example 3 :
Find the area bounded by the curve y = sin(2x) between the ordinates x = 0, x = π and x-axis.
Solution :
The points where the curve y = sin(2x) meets the x-axis can be obtained by putting y = 0.
sin 2x = 0
2x = nπ, n ∈ Z
The values of x between x = 0 are x = π are x = 0, π⁄₂, π.
The limits for the first arch are 0 and π⁄₂ and the curve lies above x-axis.
The limits for the second arch are π⁄₂ and π and the curve lies below x-axis.
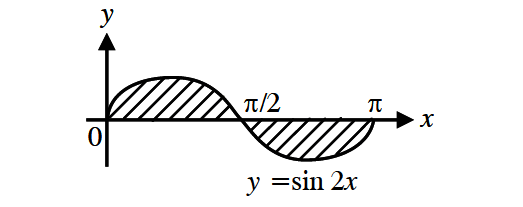
Required area is
Example 4 :
Find the area bounded by the curve y = x2 - x - 2, x-axis, x = -2, and x = 4.
Solution :
Substuite y = 0 into y = x2 - x - 2 to find at where the curve intersects x-axis.
x2 - x - 2 = 0
x2 + x - 2x - 2 = 0
x(x + 1) - 2(x + 1) = 0
(x + 1)(x - 2) = 0
x = -1 or x = 2
This curve intersects x-axis at x = -1 and x = 2.
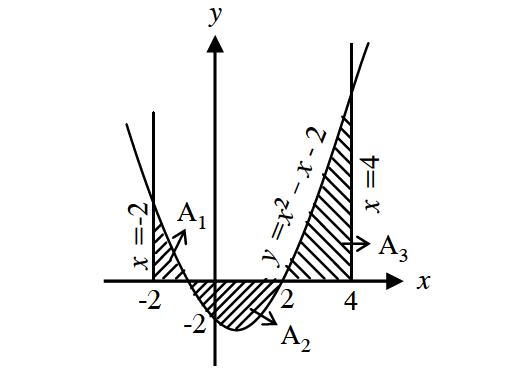
The part A2 lies below x-axis. Then, we have
Therefore, the required area is
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos
