AREA BOUNDED BY THE GIVEN LINE X AXIS AND ORDINATES
Example 1 :
Find the area of the region bounded by the line
x-y = 1
x - axis x = 2 and x = 4
Solution :
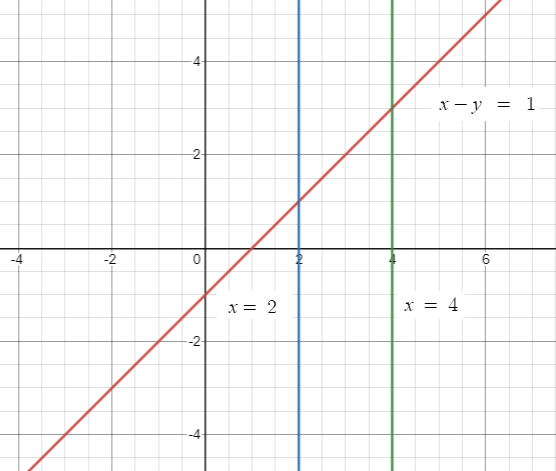
Within the limit x = 2 and x = 4, we find area under the given curve x - y = 1.
The area lies above the x-axis, so the required area is
= integral a to b y dx
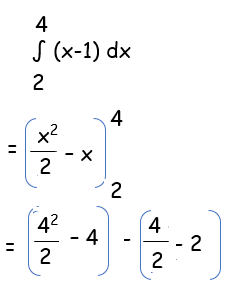
= 4 square units.
Example 2 :
Find the area of the region bounded by the line
x - y = 1
x - axis, x = - 2 and x = 0
Solution :
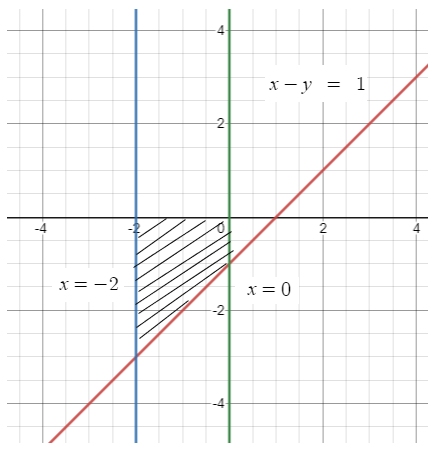
Required area = integral a to b ∫-y dx
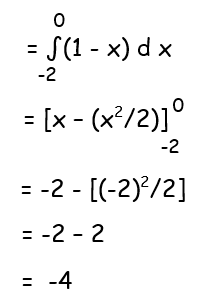
So, the required area is 4 square units.
Example 3 :
Find the area of the region by the line
x - 2y - 12 = 0
and y-axis, y = 2 and y = 5
Solution :
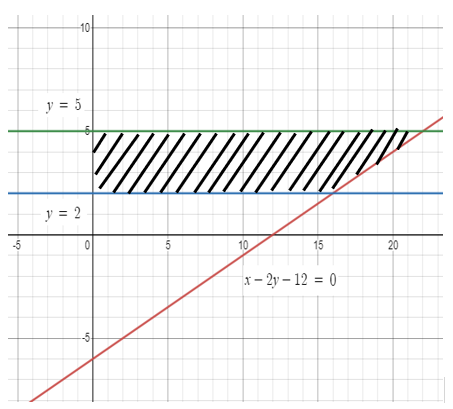
The area lies on the right side of y-axis. So,
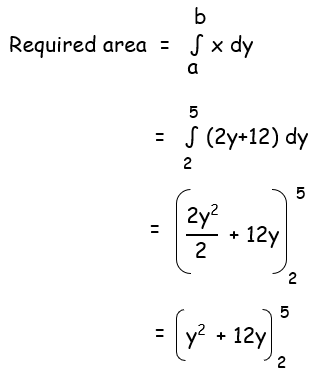
= (25 + 60) - (4 + 24)
= 85 - 28
= 57
So, the required area is 57 square units.
Example 4 :
Find the area of the region bounded by the line
y = x - 5
and the x - axis between the ordinates x = 3 and x = 7.
Solution :
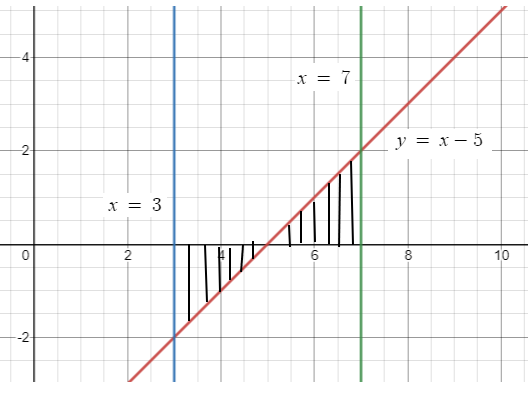
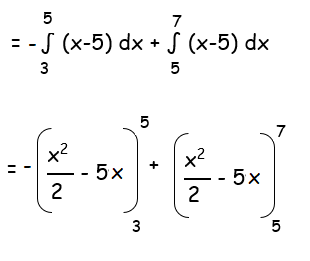
= [-(25/2) + 25] + [(9/2)-15] + [(49/2)-35] - [(25/2)-25]
= -12.5 + 25 + 4.5 - 15 + 24.5 - 35 - 12.5 + 25
= -12.5 - 15 - 35 - 12.5 + 25 + 4.5 + 24.5 + 25
= -75 + 54
= 21 square units.
Example 5 :
Find the area of the region bounded by
x2 = 36y
y - axis , y = 2 and y = 4
Solution :
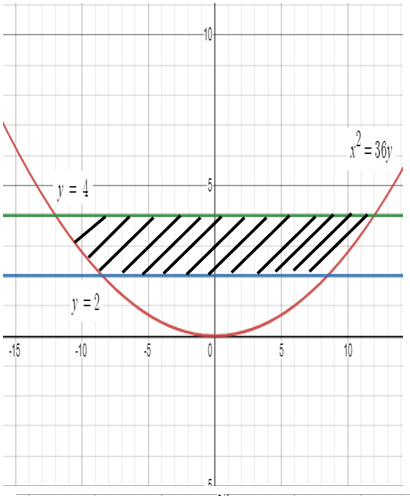
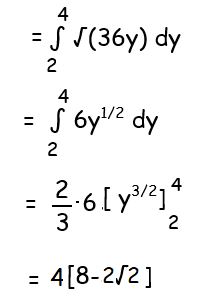
So, area of the shaded region is 8(4-√2) square units.
Example 6 :
Find the area included between the parabola
y2 = 4ax
and its latus rectum.
Solution :
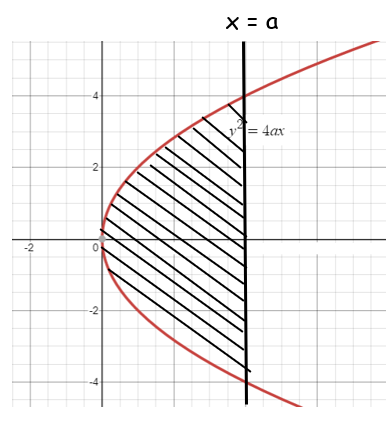
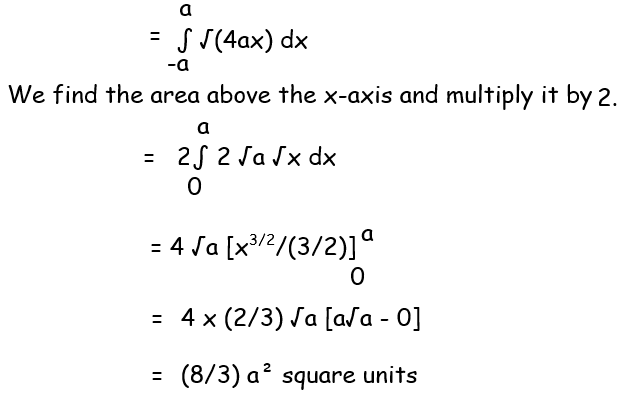
Example 7 :
Find the area of the region bounded by the ellipse
(x2/9) + (y2/5) = 1
between the two latus rectum.
Solution :
a2 = 9, b2 = 5
e = √[1-(b2/a2)]
e = √[1-(5/9)]
= √[(9-5)/9]
= √(4/9)
e = 2/3
Equation of latus rectum x = ± ae
a = 3, e = 2/3
ae = 3 (2/3)
ae = 2
Equation of latus rectum x = ± 2
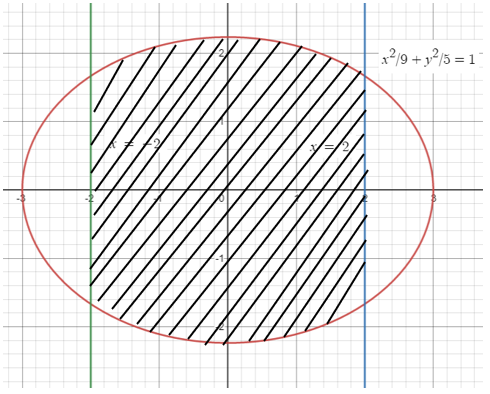
Required area = integral a to b ∫ y dx
(x2/9) + (y2/5) = 1
(y2/5) = 1 - (x2/9)
y2/5 = (9 - x2)/9
y2 = (5/9) (9-x2)
y = √(5/9) (9-x2)
y = √5/3 √(9-x2)
By using the limits x = 0 and x = 2, we can find area above the x-axis.
To find the total shaded area we have to multiply the above area by 4.
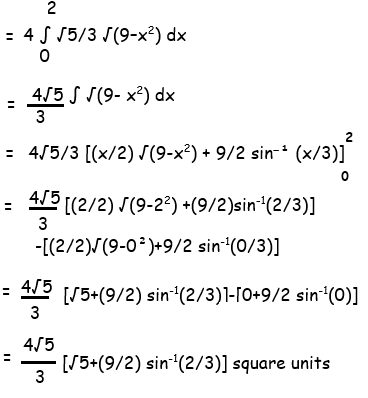
Example 8 :
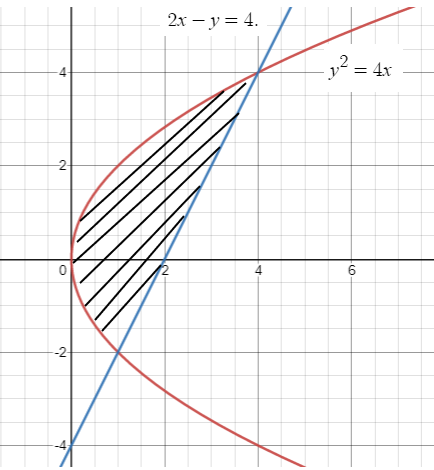
Find the area of the region bounded by the parabola
y2 = 4x
and the line
2x - y = 4
Solution :
To find the point of intersection we have to solve both equations.
x = y2/4 ------ (1)
x = (4+y)/2 ------ (2)
(1) = (2)
y2/4 = (4 + y)/2
2y2 = 4(4 + y)
2 y2 = 16 + 4 y
2y2 - 4 y - 16 = 0
now we are going to divide the whole equation by 2,
y2 - 2y - 8 = 0
(y - 4) (y + 2) = 0
y - 4 = 0 y + 2 = 0
y = 4 and y = -2
Point of intersection of two curves are (0, 4) (0, -2).
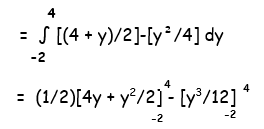
= [(32+16)/4 - (64/12) ] - [ (-16 + 4)/4 - (-8/12) ]
= [(48/4) - (16/3)] - [(-12/4) - (-8/12)]
= [12-(16/3)] - [-3 + (2/3)]
= [(36-16)/3)] - [(-9+2)/3]
= [20/3] - [-7/3]
= (20/3) + (7/3)
= (20+7)/3
= 27/3
= 9 square units
Example 9 :
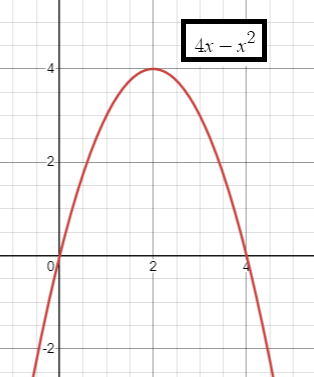
Find the area in the first quadrant bounded by
f(x) = 4x - x2
and the x-axis.
Solution :
f(x) = 4x - x2
Finding x-intercepts, we get
4x - x2 = 0
x(4 - x) = 0
x = 0 and x = 4
= 2(4)2 - 43/3 - 0
= 2(16) - (64/3)
= 32 - (64/3)
= (96 - 64)/3
= 32/3
So, the required area is 32/3 square units.
Example 10 :
Find the area bounded by the following curves
f(x) = x2 - 4, y = 0 and x = 4.
Solution :
f(x) = x2 - 4
y = x2 - 4 ------(1)
y = 0 ------(2)
Finding points of intersecting of (1) and (2), we get
x2 - 4 = 0
x2 = 4
x = √4
x = ±2
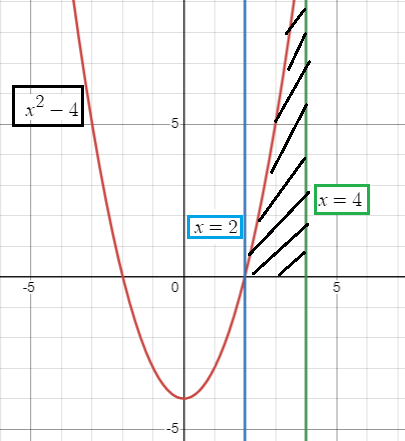
= (43/3 - 4(4)) - (23/3 - 4(2))
= (64/3) - 16 - 8/3 + 8
= (64/3) - (8/3) - 8
= (64 - 8)/3 - 8
= (56/3) - 8
= (56 - 24) / 3
= 32/3
So, the required area is 32/3 square units.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 179)
Jun 06, 25 09:14 AM
Digital SAT Math Problems and Solutions (Part - 179) -
Digital SAT Math Problems and Solutions (Part - 178)
Jun 05, 25 12:26 PM
Digital SAT Math Problems and Solutions (Part - 178) -
Digital SAT Math Problems and Solutions (Part - 177)
Jun 04, 25 10:41 AM
Digital SAT Math Problems and Solutions (Part - 177)