AREA UNDER THE CURVE USING RIGHT AND LEFT END POINTS

Consider the function y = f(x) from a to b. This means that S illustrated is the picture given below is bounded by the graph of a continuous function f, the vertical lines x = a, x = b and x axis.

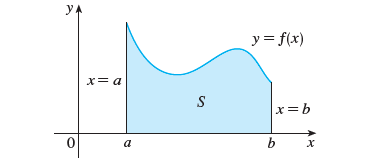
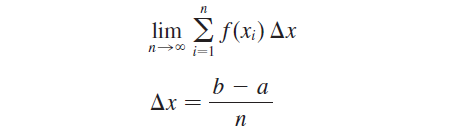
We approximate the region S by rectangles and then we take limit of the areas of these rectangles as we increase the number of rectangles. The following example illustrates the procedure.

Approximate Area Under Curve Using Left Endpoints and Right end Points

Example 1 :

Estimate the area under the graph of f(x)  =  sin x from 0 to π/2 using four approximating rectangles and

(i)  right end points 

(ii)  left end points

Solution :

Δx  =  (b - a)/n

a  =  0, b  =  π/2 and number of rectangles (n)  =  4

Δx  =  (π/2 - 0)/4

Δx  =  π/8

We can approximate each strip by that has the same base as the strip and whose height is the same as the right edge of the strip. Each rectangle has the width of π/8.

Sub intervals are [0, π/8], [π/8, π/4], [π/4,3π/8] and [3π/8, π/2].

Approximating area using right end points :

x₁  =  π/8, x₂  =  π/4, x₃  =  3π/8 and x₄  =  π/2

f(π/8)  =  sin π/8

f(π/4)  =  sin π/4

f(3π/8)  =  sin 3π/8

f(π/2)  =  sin π/2

Approximate area 

=  (π/8) [sin π/8 + sin π/4 + sin 3π/8 + sin π/2]

≈  1.1835

Approximating area using left end points :

x₁  =  0 x₂  =  π/8, x₃  =  π/4 and x₄  =  3π/8

f(0)  =  sin 0

f(π/8)  =  sin π/8

f(π/4)  =  sin π/4

f(3π/8)  =  sin 3π/8

Approximate area 

=  (π/8) [sin 0 + sin π/8 + sin π/4 + sin 3π/8]

≈  0.7908

0.7908 < Required area < 1.1835

Example 2 :

Estimate the area under the graph f(x)  =  1 + x² from x = -1 to x = 2 using three rectangles using right end points.

Solution :

Δx  =  (b - a)/n

a  =  -1, b  =  2 and number of rectangles (n)  =  3

Δx  =  (2 + 1)/3

Δx  =  1

We can approximate each strip by that has the same base as the strip and whose height is the same as the right edge of the strip. Each rectangle has the width of 1.

Sub intervals are [-1, 0], [0, 1] and [1, 2].

Approximating area using right end points :

x₁  =  0, x₂  =  1, and x₃  =  2

f(x)  =  1 + x² 

f(0)  =  1 + 0²   =  1

f(1)  =  1 + 1²   =  2

f(2)  =  1 + 2²   =  5

Approximate area 

=  1 (1 + 2 + 5)

≈  8

So the approximate area is 8.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.