AREAS OF TRIANGLES AND QUADRILATERALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In this section, you will learn how to find area of triangles and quadrilaterals.
The following postulates can be used to prove several area theorems.
Area Postulates
Area of a Square Postulate :
The area of a square is the square of the length of its side, or A = s2.
Area Congruence Postulate :
If two polygons are congruent, then they have the same area.
Area Addition Postulate :
The area of a region is the sum of the areas of its non overlapping parts.
Area Theorems
Theorem 1 (Area of a Rectangle) :
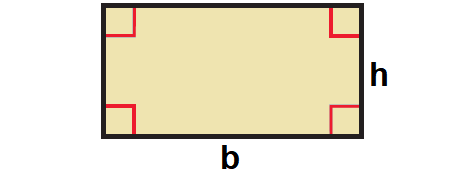
The area of a rectangle is the product of its base and height.
That is,
Area = b ⋅ h
Theorem 2 (Area of a Parallelogram) :
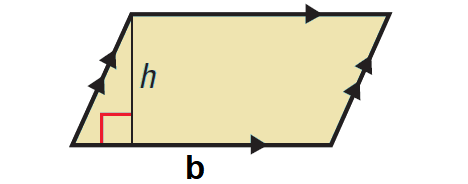
The area of a parallelogram is the product of a base and its corresponding height.
That is,
Area = b ⋅ h
Theorem 3 (Area of a Triangle) :
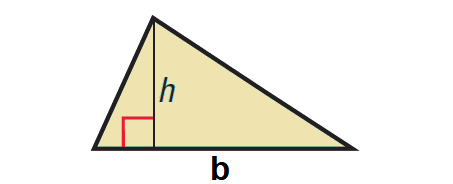
The area of a triangle is one half the product of a base and its corresponding height.
That is,
Area = 1/2 ⋅ b ⋅ h
Theorem 4 (Area of a Trapezoid) :
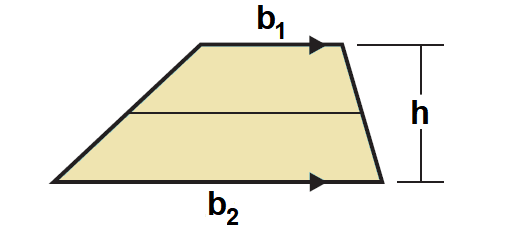
The area of a trapezoid is one half the product of the height and sum of the bases.
That is,
Area = 1/2 ⋅ h ⋅ (b1 + b2)
Theorem 5 (Area of a Kite) :
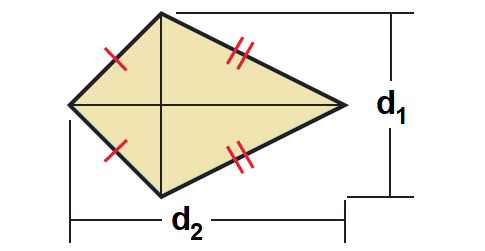
The area of a kite is one half the product of the lengths of its diagonals.
That is,
Area = 1/2 ⋅ d1 ⋅ d2
Theorem 6 (Area of a Rhombus) :
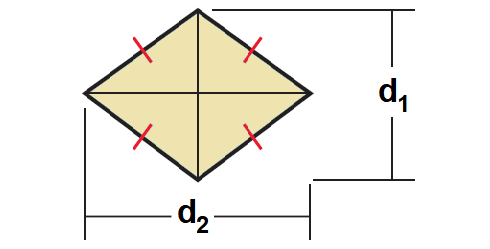
The area of a rhombus is one half the product of the lengths of its diagonals.
That is,
Area = 1/2 ⋅ d1 ⋅ d2
Proof of the Area a Parallelogram
The area of a parallelogram is the area of a rectangle with the same base and height.
It has been illustrated in the diagram given below.

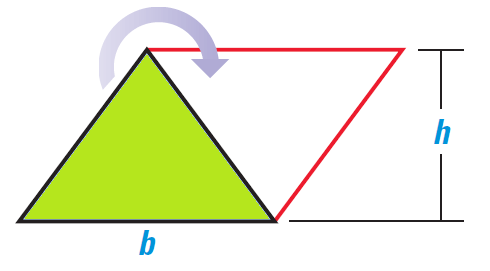
Proof of the Area a Triangle
The area of a triangle is half the area of a parallelogram with the same base and height.
It has been illustrated in the diagram given below.
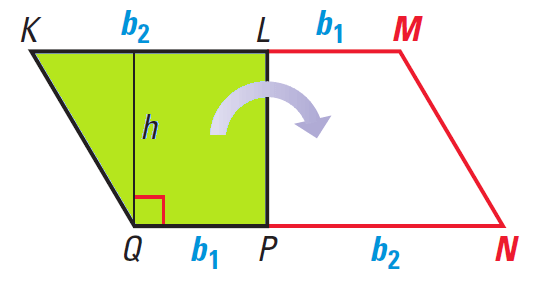
Proof of the Area a Trapezoid
The area of a trapezoid is half the area of the parallelogram with the same height and a base length is equal to sum of the base lengths of the trapezoid.
It has been illustrated in the diagram given below.
Proof of the Area a Kite
The area of a kite is half the area of the rectangle whose length and width are the lengths of the diagonals of the kite.
It has been illustrated in the diagram given below.
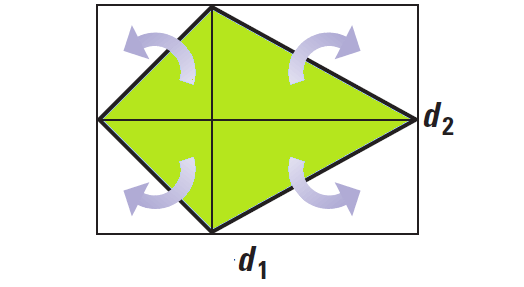
Proof of the Area a Rhombus
The area of a rhombus is half the area of the rectangle whose length and width are the lengths of the diagonals of the rhombus.
It has been illustrated in the diagram given below.
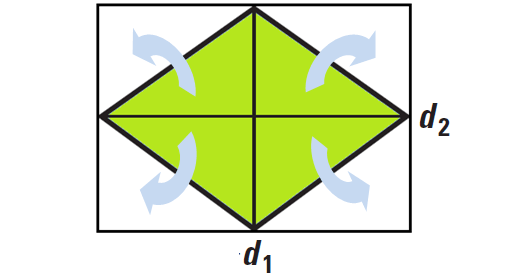
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
