AREAS OF TRIANGLES AND QUADRILATERALS WORKSHEET

Problem 1 :

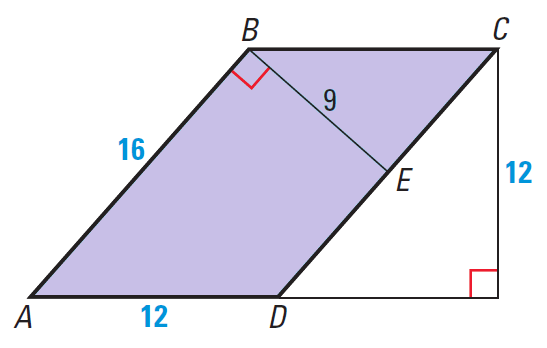
Find the area of the figure ABCD shown below.

Problem 2 :

Find the height of a triangle that has an area of 12 square units and base length is 6 units.

Problem 3 :

A triangle has an area of 52 square feet and a base of 13 feet. Are all triangles with these dimensions congruent.

Problem 4 :

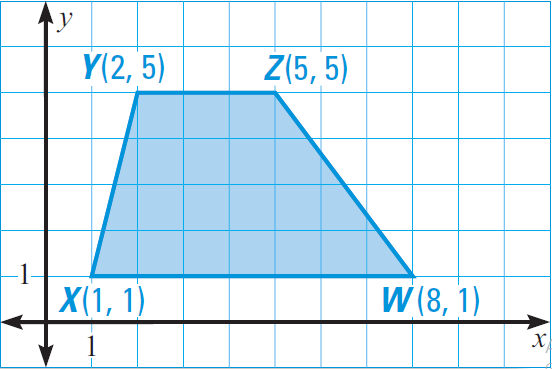
Find the area of trapezoid WXYZ shown below.

Problem 5 :

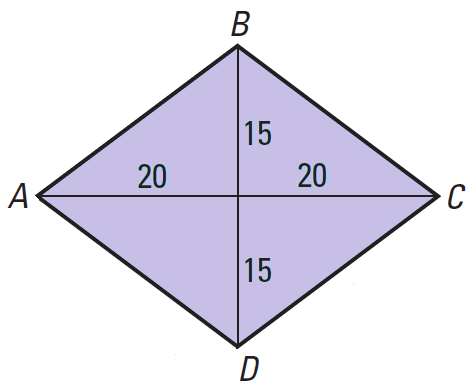
Find the area of the rhombus ABCD shown below.

Problem 6 :

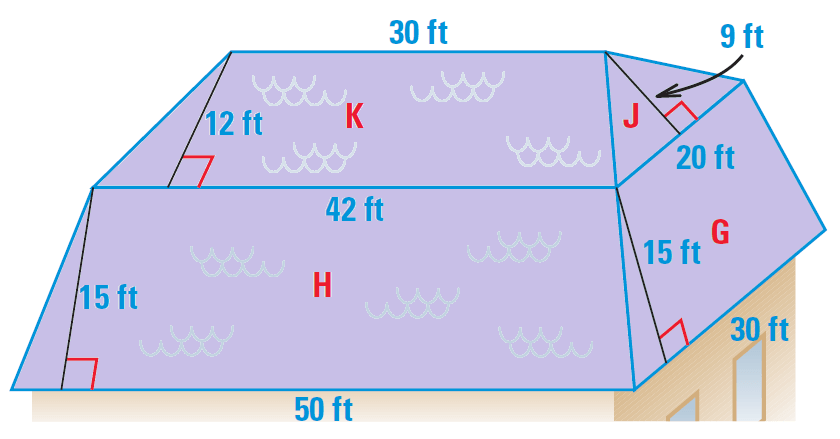
Find the area of roof of the house shown below.

1. Answer :

Method 1 :

Use AB as the base. Then, b = 16 and h = 9.

Area of the figure ABCD is

= b ⋅ h

= 16 ⋅ 9

= 144 square units

Method 2 :

Use AD as the base. Then, b = 12 and h = 12.

Area of the figure ABCD is

= b ⋅ h

= 12 ⋅ 12

= 144 square units

Notice that we get the same area with either base.

2. Answer :

Because we want to find height of the triangle, we have to rewrite the area formula such that h is alone on one side of the equation.

Formula to find area of a triangle :

A = 1/2 ⋅ b ⋅ h

Multiply both sides by 2.

2A = b ⋅ h

Divide both sides by b.

2A/b = h

Given : A = 12 and b = 6.

Then, we have

(2 ⋅ 12)/6 = h

4 = h

So, the height of the triangle is 4 units.

3. Answer :

Because we want to find height of the triangle, we have to rewrite the area formula such that h is alone on one side of the equation.

Using formula from Problem 2, the height of the triangle is

h = (2 ⋅ 52)/13

h = 8 feet

There area many triangles with these dimensions. Some are shown below.

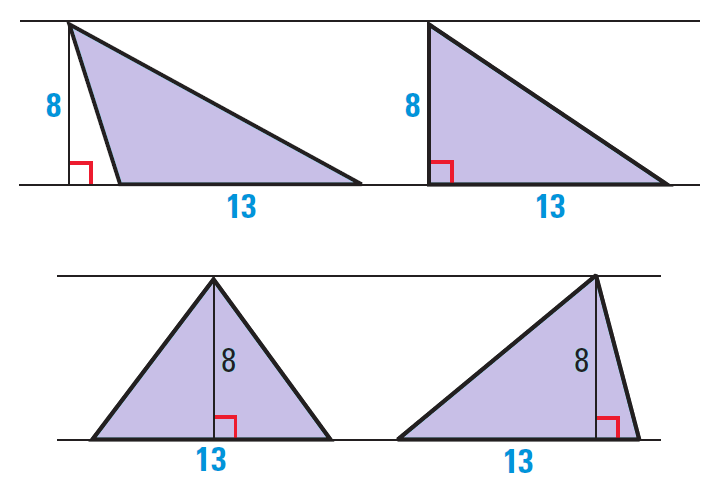
4. Answer :

The height of the trapezoid WXYZ above is

h = 5 - 1

h = 4 units

Find the lengths of the bases :

Formula to find area of a trapezoid :

A = 1/2 ⋅ h ⋅ (b₁ + b₂)

Substitute h = 4, b₁ = 3 and b₂ = 7.

A = 1/2 ⋅ 4 ⋅ (3 + 7)

A = 20

So, the area of trapezoid WXYZ is 20 square units.

5. Answer :

Let d₁ and d₂ represent lengths of the diagonals AC and BD respectively.

d₁ = AC = 20 + 20 = 40 units

d₁ = BD = 15 + 15 = 30 units

Formula to find area of a rhombus :

A = 1/2 ⋅ d₁ ⋅ d₂

Substitute d₁ = 40 and d₂ = 30.

A = 1/2 ⋅ 30 ⋅ 40

A = 600

So, the area of rhombus ABCD is 600 square units.

6. Answer :

G, H and K are trapezoids and J is a triangle. The hidden back and left sides of the roof are the same as the front and right sides.

Area of J = 1/2 ⋅ 20 ⋅ 9 = 90 ft²

Area of G = 1/2 ⋅ 15 ⋅ (20 + 30) = 375 ft²

Area of H = 1/2 ⋅ 15 ⋅ (42 + 50) = 690 ft²

Area of K = 1/2 ⋅ 12 ⋅ (30 + 42) = 432 ft²

The roof has two congruent faces of each type.

So, the total area is

= 2(90 + 375 + 690 + 432)

= 2(1587)

= 3174

So, the total area of the roof is 3174 square feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.