AREA OF TRIANGLE WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Each triangular face of the Pyramid of Peace in Kazakhstan is made up of 25 smaller equilateral triangles. These triangles have measurements as shown in the diagram. What is the area of one of the smaller equilateral triangles ?
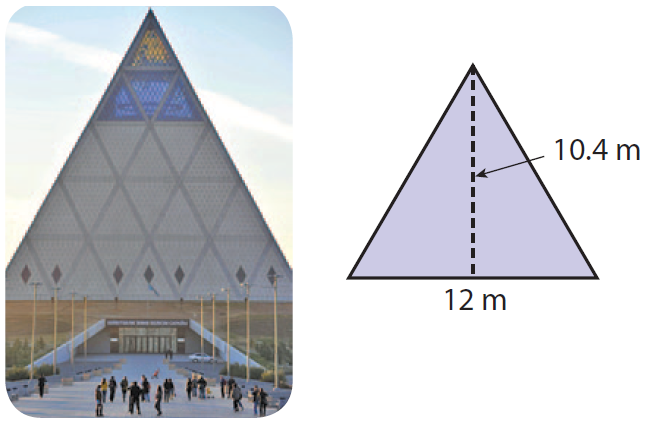
Solution :
Area of smaller equilateral triangle is
= (1/2) x b x h
Substitute 2 for b and 10.4 for h.
= (1/2) x 12 x 10.4
= 6 x 10.4
= 62.4 square meter
Problem 2 :
Amy needs to order a shade for a triangular-shaped window that has a base of 6 feet and a height of 4 feet. What is the area of the shade ?
Solution :
Since the shade is in the shape of triangle, we have to use the formula for area of triangle to find the area of the shade.
Area of the shade is
= (1/2) x b x h
Substitute 6 for b and 4 for h.
= (1/2) x 6 x 4
= 12 square feet
Example 3 :
Monica has a triangular piece of fabric. The height of the triangle is 15 inches and the triangle’s base is 6 inches. Monica says that the area of the fabric is 90 square inches . What error did Monica make ? Explain your answer.
Solution :
Area of the triangle is
= (1/2) x b x h
Substitute 6 for b and 15 for h.
= (1/2) x 6 x 15
= 15 x 3
= 45 square inches
Actual area of the triangular piece of fabric is 45 square inches. But Monica says that area of the fabric is 90 square inches. Which means, she forgot to multiply the product of base and height by 1/2. This is the error that she has made.
Example 4 :
The sixth-grade art students are making a mosaic using tiles in the shape of right triangle. The two sides that meet to form a right angle are 3 centimeters and 5 centimeters long. If there are 200 tiles in the mosaic, what is the area of the mosaic ?
Solution :
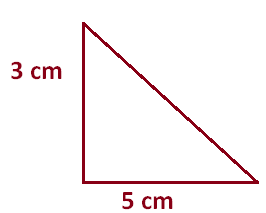
Area of each tile is
= (1/2) x b x h
Substitute 5 for b and 3 for h.
= (1/2) x 5 x 3
= 7.5 cm²
Area of 200 of the mosaic is
= 200 x 7.5
= 1500 cm²
Example 5 :
Wayne is going to paint the side of the house shown in the diagram. What is the area that will be painted? Explain how you found your answer.
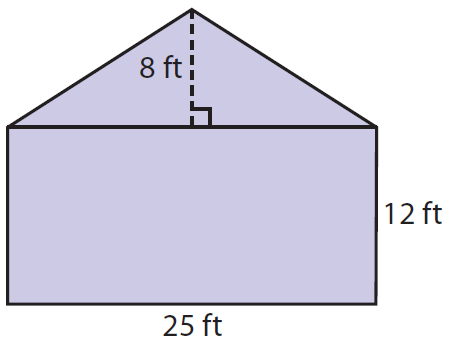
Solution :
Wayne's house in the above picture is made up of using two shapes. One is triangle and and other one is rectangle.
By finding the sum of areas of triangle and rectangle, we can get the required area that will be painted.
Required area is
= Area of triangle + Area of rectangle
= [(1/2 ) x b x h] + [l x w]
= [(1/2) x 25 x 8] + (25 x 12)
= 100 + 300
= 400 square ft
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


