AREA OF TRIANGLE USING DETERMINANT FORMULA

Here we are going to see, how to find the area of a triangle with given vertices using determinant formula.

We know that the area of a triangle whose vertices are  (x₁ , y₁),(x₂ , y₂) and (x₃ , y₃) is equal to the absolute value of

(1/2) [x₁ y₂ - x₂y₁ + x₂y₃ -  x₃y₂ + x₃y₁ - x₁y₃]

This expression can be written in the form of a determinant as shown below.

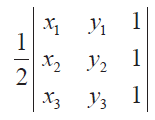
Note :

The area of the triangle formed by three points is zero if and only if the three points are collinear.

Also, we remind the reader that the determinant could be negative whereas area is always non negative.

Practice Problems

Problem 1 :

Find the area of the triangle whose vertices are (0, 0), (1, 2) and (4, 3).

Solution :

Let the point be (x₁, y₁)  ==>  (0, 0), (x₂, y₂) ==> (1, 2) and (x₃, y₃) ==> (4, 3)

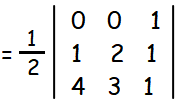
  =  (1/2)[3 - 8]

  =  (1/2)[-5]

  =  5/2

=  2.5

Area cannot be represented with negative. So, area of the triangle with given vertices is 2.5 square units.

Problem 2 :

If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.

Solution :

Area of triangle  = 4 square units 

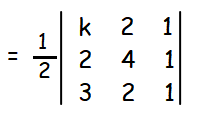
(1/2){k [4 - 2] - 2[2 - 3] + 1[4 - 12] } =  4

k(2) - 2(-1) + 1(-8)  =  8

 2k + 2 - 8 =  8

2k - 6  =  8

2k  =  8 + 6

2k  =  14

k  =  7

So, the value of k is 7.

Problem 3 :

Find the area of the triangle whose vertices are (-2, -3), (3, 2), and (-1, -8).

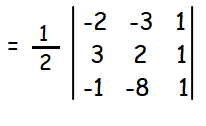
  =  (1/2) [ -2(2 + 8) + 3(3+1) + 1(-24 + 2) ]

  =  (1/2) [-2 (10) + 3(4) + 1(-22)]

  =  (1/2) [ -20 + 12 - 22]

  =  (1/2) [ -42 + 12]

  =  (1/2) (-30)

  =  -15

So, the required area is 15 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.