AREA OF SQUARE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Find the area of the square having side length 24 cm.
Problem 2 :
If the area of a square is 64 square inches, then find the length of each side.
Problem 3 :
Find the area of the figure shown below.
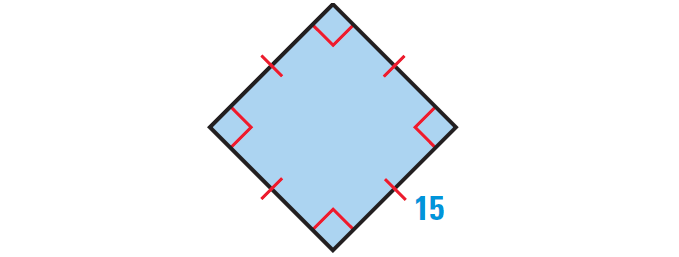
Problem 4 :
The square has side length of 250 cm. Find its area in square meter.
Problem 5 :
If the length of each diagonal is 2√2 cm, then find its area.
Problem 6 :
If the perimeter of a square is 30 inches, then find its area.
Problem 7 :
Find the area of the figure which has the following vertices in xy-coordinate plane.
E(-1, 3), F(4, 3), G(4, -2) and H(-1, -2)
Problem 8 :
PQ is one of the sides of the square PQRS and the side PQ is defined by P(0, 2) and C(6, 9). Find the area of the square PQRS.
Problem 9 :
AC is one of the diagonals of the square ABCD and the diagonal AC is defined by A(1, 4) and C(4, 8). Find the area of the square ABCD.
Problem 10 :
If the lengths of the diagonals of two squares are in the ratio 2 : 5. then find the ratio of their areas.

1. Answer :
When the length of a side is given, formula for area of a square :
= s2
Substitute 24 for s.
= 242
= 576
So, the area of the square is 576 square cm.
2. Answer :
Area of the square = 64 in2
s2 = 64
Find positive square root on both sides.
√s2 = √(8 ⋅ 8)
s = 8
So, the length of each side of the square is 8 inches.
3. Answer :

The figure shown above is a four sided closed figure. The lengths of all the four sides are equal and each vertex angle is right angle or 90o.
Therefore, the figure shown above is a square with side length 15 units.
When the length of a side is given, formula for area of a square :
= s2
Substitute 15 for s.
= 152
= 225
So, the area of the figure shown below is 225 square units.
4. Answer :
When the length of a side is given, formula for area of a square :
= s2
Substitute 250 for s.
= 2502
= 62500 cm2 ----(1)
We know
100 cm = 1 m
Square both sides.
(100 cm)2 = (1 m)2
1002 cm2 = 12 m2
10000 cm2 = 1 m2
Therefore, to convert centimeter square into meter square, we have to divide by 10000.
(1)----> Area of the square = 62500 cm2
Divide the right side by 10000 to convert cm2 into m2.
Area of the square = (62500/10000) m2
= 6.25 m2
So, the area of the square is 6.25 square meter.
5. Answer :
When the length of a diagonal is given, formula for area of a square :
= 1/2 ⋅ d2
Substitute 2√2 for d.
= 1/2 ⋅ (2√2)2
Simplify.
= 1/2 ⋅ (4 ⋅ 2)
= 1/2 ⋅ (8)
= 4
So, the area of the square is 4 square cm.
6. Answer :
Perimeter = 30 inches
4s = 30
Divide each side by 4.
s = 7.5
When the length of a side is given, formula for area of a square :
= s2
Substitute 7.5 for s.
= 7.52
= 56.25
So, the area of the square is 56.25 square inches.
7. Answer :
E(-1, 3), F(4, 3), G(4, -2) and H(-1, -2)
Draw a sketch with the given vertices.
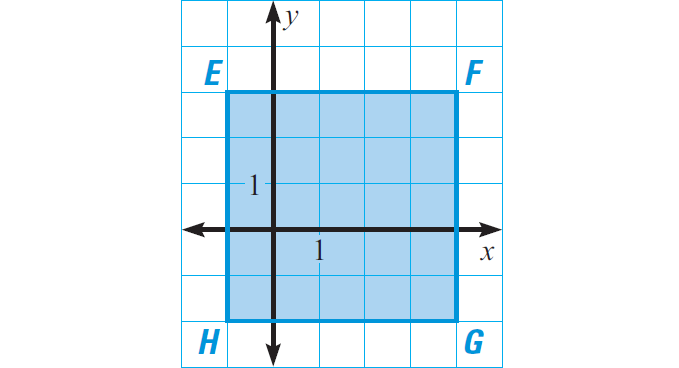
Clearly, the above figure is a square with side length of 5 units.
When the length of a side is given, formula for area of a square :
= s2
Substitute 5 for s.
= 52
= 25
So, the area of the square is 25 square units.
8. Answer :
P(0, 2) and C(6, 9)
Distance between the two points (x1, y1) and (x2, y2) is
= √[(x2 - x1)2+(y2 - y1)2]
To find the distance between P and Q, substitute
(x1, y1) = (0, 2)
(x2, y2) = (6, 9)
in the above formula.
Distance between P and Q :
= √[(6-0)2 + (9-2)2]
= √[62 + 72]
= √[36 + 49]
= √85
Therefore, the length of the side PQ is √85 units.
When the length of a side is given, formula for area of a square :
= s2
Substitute s = √85.
= (√85)2
= 85
So, the area of the square PQRS is 85 square units.
9. Answer :
A(1, 4) and C(4, 8)
Distance between the two points (x1, y1) and (x2, y2) is
= √[(x2 - x1)2+(y2 - y1)2]
To find the distance between A and C, substitute
(x1, y1) = (1, 4)
(x2, y2) = (4, 8)
in the above formula.
Distance between A and C :
= √[(4-1)2 + (8-4)2]
= √[32 + 42]
= √[9 + 16]
= √25
= 5
Therefore, the length of the diagonal AC is 5 units.
When the length of a diagonal is given, formula for area of a square :
= 1/2 ⋅ d2
Substitute d = 5.
= 1/2 ⋅ 52
Simplify.
= 1/2 ⋅ 25
= 12.5
So, the area of the square ABCD is 12.5 square units.
10. Answer :
From the ratio 2 : 5, let the diagonals of two squares be 2x and 5x respectively.
When the length of a diagonal is given, formula for area of a square :
= 1/2 ⋅ d2
|
Area of 1st square = 1/2 ⋅ (2x)2 = 1/2 ⋅ (4x2) = 4x2/2 |
Area of 2nd square = 1/2 ⋅ (5x)2 = 1/2 ⋅ (25x2) = 25x2/2 |
Ratio of the areas :
= (4x2/2) : (25x2/2)
Multiply each term of the ratio by 2.
= 4x2 : 25x2
Divide each term by x2.
= 4 : 25
So, the ratio of the areas of two squares is 4 : 25.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems