AREA OF RECTANGLE WORKSHEET

1. Find the area of a rectangle, if its length is 15 cm and width is 20 cm.

2. The length of a rectangle is 3 times its width. If its perimeter is 32 ft., then find the area of the rectangle.  

3. If the length of each diagonal of a rectangle is 13 cm and its width is 12 cm, then find the area of the rectangle. 

4. The difference between the length and width of a rectangle is 1 cm. If the length of one of the diagonals is 5 cm, then find the area of the rectangle. 

5. The length and width of a rectangle are in the ratio 3 : 4 and its area is  588 square inches. Find its length and width. 

6. Find the cost of carpeting the floor of a room whose length is 13 m and width is 9 m. If the cost of the carpet is $12.40 per square meter, find the total cost of carpeting the floor of the room. 

7. The length of  a rectangle is 70 cm and width is 30 cm. If the length is increased by 10% and width is by 20%, then find the percentage increase in area. 

8. The length of  a rectangle is 80 cm and width is 40 cm. If the length is increased by 20% and width is decreased by 10%, By what percentage will the area be increased or decreased ?

1. Answer :

Formula for area of a rectangle :

=  l ⋅ w

Substitute 15 for l and 20 for w.

=  15 ⋅ 20

=  300 cm²

2. Answer :

Let x be the width of the rectangle.

Then, its length is 3x.

Perimeter of the rectangle is 32 ft

2(l + w) = 32

Divide each side by 2.

l + w = 16

Substitute 3x for l and x for w.

3x + x = 16

4x = 16

Divide each side by 4.

x = 4

Therefore, width of the rectangle is 4 ft.

And length of the rectangle is

= 3(4)

= 12 ft

Formula for area of a rectangle :

= l ⋅ w

Substitute 12 for l and 4 for w.

= 12 ⋅ 4

= 48 ft²

3. Answer :

To find the area of a rectangle, we have to know its length and width. Width is given in the question, that is 12 cm. So, find its length.

Draw a sketch.

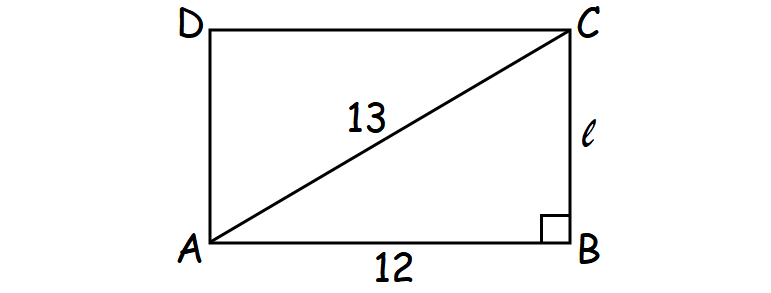
In the figure shown above, consider the right triangle ABC.

By Pythagorean Theorem, we have

AB² + BC² = AC²

Substitute.

12² + l² = 13²

Simplify and solve for l.

144 + l² = 169

Subtract 144 from each side.

l² = 25

Find positive square root on both sides.

 √l² = √25

l = 5

Therefore, the length of the rectangle is 5 cm.

Formula for area of a rectangle :

= l ⋅ w

Substitute 5 for l and 12 for w.

= 5 ⋅ 12

= 60 cm²

4. Answer :

Because the difference between the length and width of a rectangle is 1 cm, we can assume the length of the rectangle as x cm and width as (x + 1) cm.

Draw a sketch.

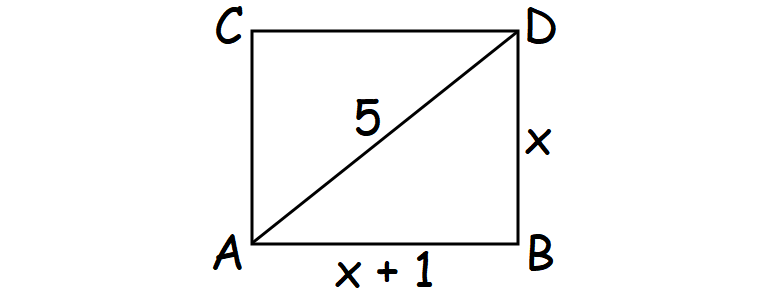
In the figure shown above, consider the right triangle ABC.

By Pythagorean Theorem, we have

AB² + BC² = AC²

Substitute.

(x + 1)² + x² = 5²

Simplify and solve for x.

x² + 2 ⋅ x ⋅ 1 + 1² + x² = 25

x² + 2x + 1 + x² = 25

2x² + 2x + 1 = 25

Subtract 25 from each side.

2x² + 2x - 24 = 0

Divide each side by 2.

x² + x - 12 = 0

Factor.

(x + 4)(x -3) = 0

x + 4 = 0 or x - 3 = 0

x = - 4 or x = 3

Because the length of a rectangle can not be negative, we can ignore x = - 4.

So, length is 3 cm.

Then the width is

= x + 1

= 3 + 1

= 4 cm

Formula for area of a rectangle :

= l ⋅ w

Substitute 3 for l and 4 for w.

= 3 ⋅ 4

= 12 cm²

5. Answer : 

From the ratio 3 : 4, let the length and width of the rectangle be 3x and 4x respectively.

Area of the rectangle = 588 in²

l ⋅ w = 588

Substitute 3x for l and 4x for w.

3x ⋅ 4x = 588

12x² = 588

Divide each side by 12.

x² = 49

Find positive square root on both sides.

 √x² = √49

x = 7

Length = 3x = 3(7) = 21 in

Width = 4x = 4(7) = 28 in

6. Answer : 

To find the total cost of carpeting the floor of the room, we have to know its area. Because the floor of the room is in rectangle shape, we can use the formula for area of a rectangle to find the area of the floor.    

Formula for area of a rectangle :

= l ⋅ w

Substitute 13 for l and 9 for w.

= 13 ⋅ 9

= 117

So, the area of the floor is 117 square meters.

The cost of carpet is $12.40 per square meter. 

Then, the total cost of carpet for 117 square meters : 

= 117 ⋅ 12.40

= $1450.80

7. Answer :

Before increase in length and width :

Formula for area of a rectangle :

= l ⋅ w

Substitute 70 for l and 30 for w.

= 70 ⋅ 30

= 2100 

Therefore, the area of the rectangle is 2100 square cm.

After increase in length and width :

Length = (100 + 10)% of 70 = 1.1 ⋅ 70 = 77 cm

Width = (100 + 20)% of 30 = 1.2 ⋅ 30 = 36 cm

Formula for area of a rectangle :

= l ⋅ w

Substitute 77 for l and 36 for w. 

= 77 ⋅ 36

= 2772 cm²

Percentage increase in area :

Increase in area = 2772 - 2100

= 672 cm²

Percentage increase in area = (672 / 2100) ⋅ 100 %

= 32%

8. Answer :

Before changes in length and width :

Formula for area of a rectangle :

= l ⋅ w

Substitute 80 for l and 40 for w.

= 80 ⋅ 40

= 3200

Therefore, the area of the rectangle is 3200 square cm.

After changes in length and width :

Length = (100 + 20)% of 80 = 1.2 ⋅ 80 = 96 cm

Width = (100 - 10)% of 40 = 0.9 ⋅ 40 = 36 cm

Formula for area of a rectangle :

= l ⋅ w

Substitute 96 for l and 36 for w.

= 96 ⋅ 36

= 3456 cm²

Difference in area :

= 3456 - 3200

= 256 cm²

After 20% increase in length and 10% decrease in width, the area of the rectangle is increase by 256 square cm. 

Percentage increase in area :

= (256/3200) ⋅ 100 %

= 8%

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.