AREA OF COMPOSITE FIGURES 

Example 1 : 

Find the area of the figure shown below.

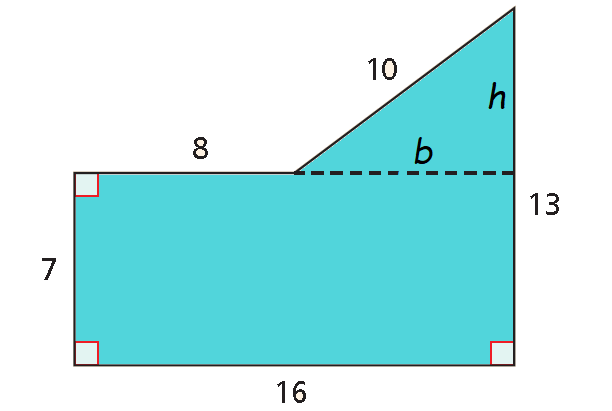
Solution : 

Divide the figure into a rectangle and a right triangle. Notice that you do not know the base and the height of the triangle. Use b and h to represent these lengths.

The bottom of the rectangle is 16 units long ; the top of the rectangle is 8 units long plus the base of the triangle. Use this information to write and solve an equation.

b + 8  =  16

Subtract 8 from each side. 

b  =  8

The right side of the figure is 13 units long : 7 units from the rectangle plus the height of the triangle. Use this information to write and solve an equation.

h + 7  =  13

Subtract 7 from each side.

h  =  6

The area of the figure is the sum of the areas of the rectangle and the triangle.

A  =  Area of rectangle + Area Triangle

=  lw + bh/2

=  (16 ⋅ 7) + (8 ⋅ 6)/2

=  112 + 48/2

=  112 + 24

=  136 square units

Example 2 : 

Find the area of the figure shown below.

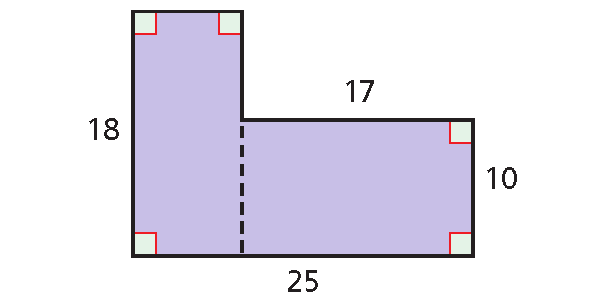
Solution : 

Divide the figure into two rectangles. Notice that you do not know length of the rectangle on the left.

The bottom of the figure is 25 units long ; the length of the rectangle on the right is 17 units. Use this information to find the length of the rectangle on the left. 

Length of rectangle on the left  =  25 - 17

=  8 units

The area of the figure is the sum of the areas of the two rectangles.

A  =  Area of rectangle (left) + Area of Rectangle (right)

=  lw + lw

=  (8 ⋅ 18) + (17 ⋅ 10)

=  144 + 170

=  314 square units

Example 3 : 

Find the area of the figure shown below.

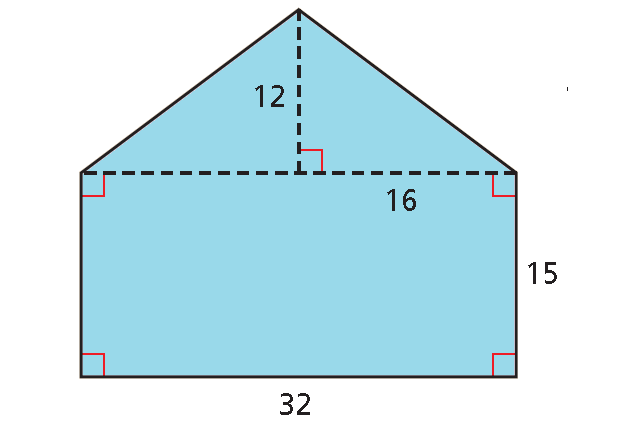
Solution : 

Divide the figure into a rectangle and a triangle. Notice that you do not know the base of the triangle. 

The length of the rectangle is 32 units long. The base of the triangle and length of the rectangle are equal in length. 

So, base of the triangle is 32 units.

The area of the figure is the sum of the areas of the rectangle and the triangle.

A  =  Area of rectangle + Area Triangle

=  lw + bh/2

=  (32 ⋅ 15) + (12 ⋅ 32)/2

=  480 + 192

=  672 square units

Example 4 : 

Find the area of the figure shown below.

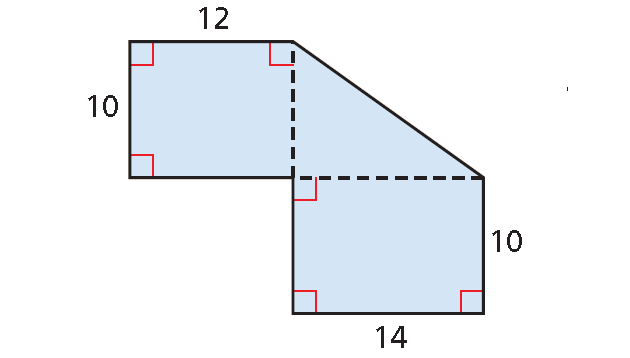
Solution : 

Divide the figure into a rectangle, a triangle and a rectangle. Notice that you do not know the base and height of the triangle. 

The width of the rectangle at the top is 10 units long. The height of the triangle and width of the rectangle are equal in length. 

So, height of the triangle is 10 units.

The length of the rectangle at the bottom is 14 units long. The base of the triangle and length of the rectangle are equal in length. 

So, base of the triangle is 14 units.

The area of the figure is the sum of the areas of the rectangle, triangle and rectangle.

A  =   lw + bh/2 + lw

=  (12 ⋅ 10) + (14 ⋅ 10)/2 + (14 ⋅ 10)

=  120 + 140/2 + 140

=  120 + 70 + 140

=  330 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.