AREA OF COMPOSITE FIGURES 7TH GRADE

Example 1 :

Find the area of the figure shown below. 

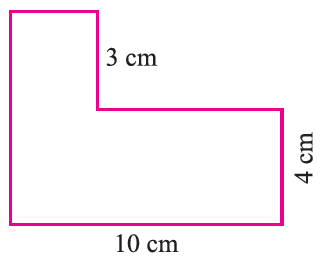
Solution :

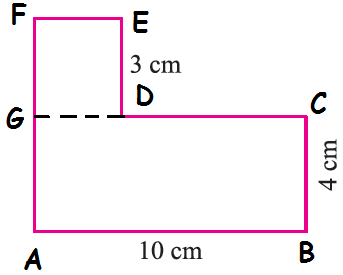
By drawing a line GD parallel to AB, we can split the given picture as two parts.

(i) GDEF is a square of side length 3 cm

(ii) ABCG is a rectangle of length 10 cm and width 4 cm

Area of square  =  a²

Area of rectangle  =  length ⋅ breadth

Area of square (GDEF)  =  3²  =  9 cm²

Area of rectangle  =  10 ⋅ 4  =  40 cm²

Area of the given figure  =  40 + 9  =  49 cm²

Example 2 :

Find the area of the figure shown below. 

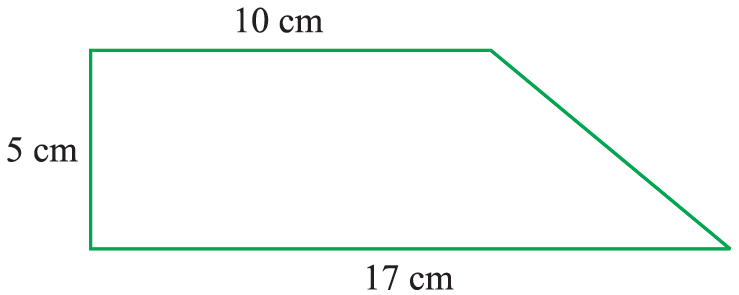
Solution :

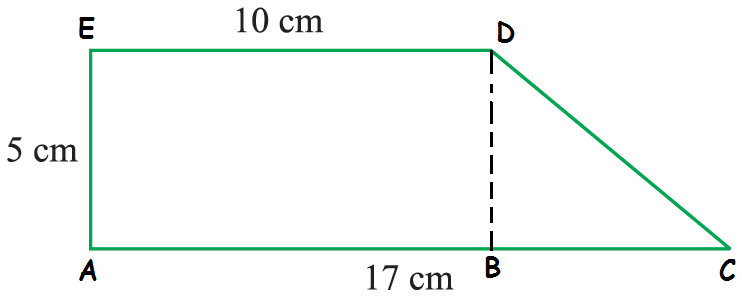
By drawing a line BD parallel to AE, we can split the given picture as two parts.

(i) BCD is a triangle

(ii) ABED is a rectangle 

Area of triangle  =  (1/2) ⋅ b ⋅ h

Area of rectangle  =  length ⋅ breadth

length of AC  =  17

AB + BC  =  17  ==> 10 + BC  =  17 ==> BC  =  7 cm

Area of triangle  =  (1/2) ⋅ 7 ⋅ 5  =  35/2  ==>  17.5 cm²

Area of rectangle  =  10 ⋅ 5  =  50 cm²

Area of given shape  =  17.5 + 50  ==>  67.5 cm²

Example 3 :

John bought a square plot of side 60 m. Adjacent to this David bought a rectangular plot of dimension 70 m x 50 m. Both paid the same amount. Who is benefited ?

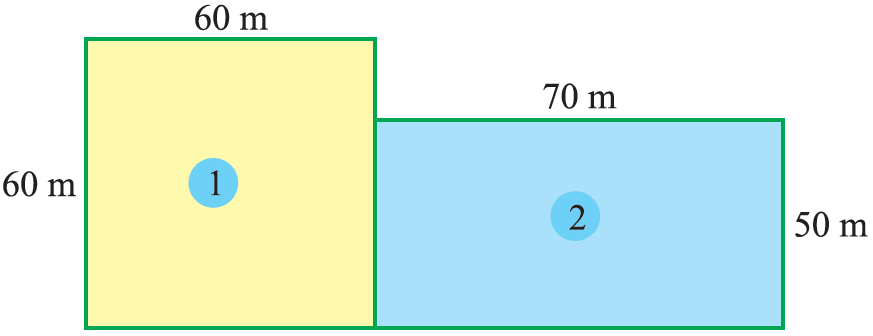
Solution :

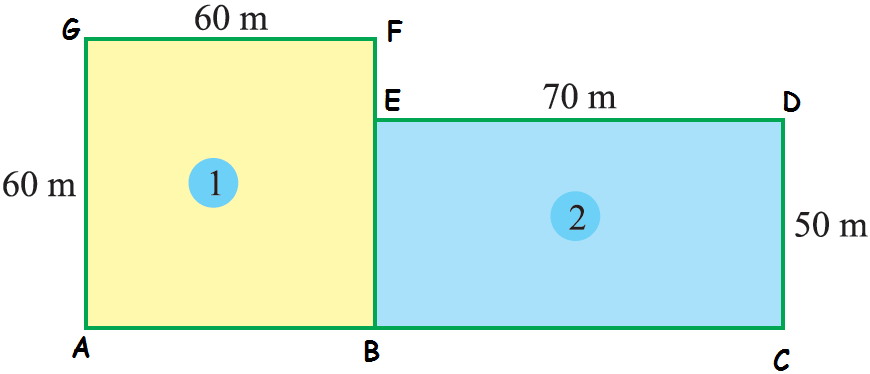
To find who is benefited, we have to find the area of above shapes separately. 

(i) ABFG is a square of side length 60 m

(ii) BCDE is a rectangle of length 70 m and width 50 m.

Area of square   =  a²

Area of rectangle  =  length x breadth

Area of ABFG  =  60²  =  60 x 60  =  3600 m²

Area of rectangle  =  70 x 50  =  3500 m²

From the above calculation, we come to know that John is having more area than David. So John is more benefited.

Example 4 :

Find the area of the figure shown below. 

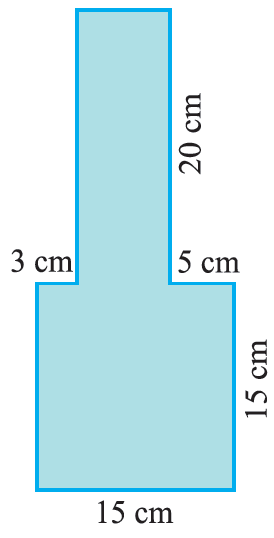
Solution :

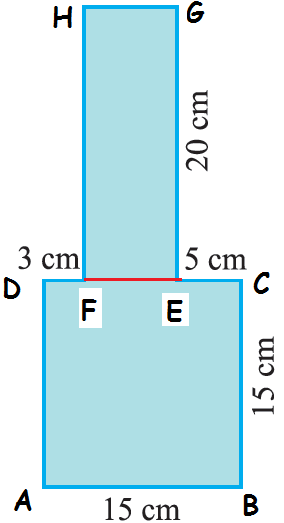
(i)  ABCD is a square of side length 15 cm

(ii)  Area of rectangle FEGH  

Length of DC  =  15

DF + FE + EC  =  15  ==> 3 + FE + 5  =  15

FE  =  15 - 8  ==> FE  =  7 cm

Area of square (ABCD)  =  a²  ==>  15²  ==>  225 cm²

Area of rectangle (FEGH)  =  length x width

  =  20 x 7  =  140 cm²

Area of the given figure  =  225 + 140  =  365 cm²

Example 5 :

Daniel bought a square plot of side 50 m. Adjacent to this Richard bought a rectangular plot of length 60 m and breadth 40 m for the same price. Find out who is benefited and how many sq. m. are more for him?

Solution :

Area of square plot = a².

Side length of square = 50 m.

Area of land owned by Daniel = 50².  

= 50 ⋅ 50

= 2500 m²

Area of land owned by Richard = length ⋅ width

  =  60 ⋅ 40

=  2400 m²

Since Daniel is having more area than Richard, we can decide that Daniel is benefited.

Daniel is having 100 m² more area than Richard.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.