AREA OF POLYGONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A polygon is a plane shape with straight sides. The area of a polygon measures the size of the region enclosed by the polygon. It is measured in units squared.
Area of Equilateral Triangle
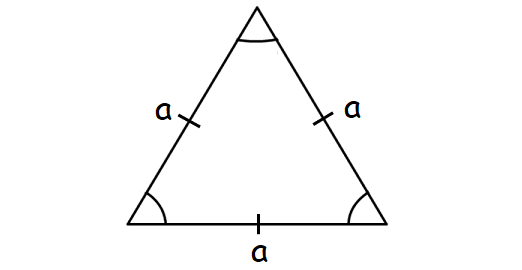
A triangle with all three sides of equal length. All the angles are 60°.
Formula for area of an equilateral triangle :
= (√3/4)a2
Area of Scalene Triangle
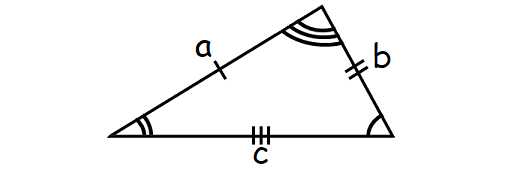
A scalene triangle is a triangle that has three unequal sides.
Formula for area of a scalene triangle :
= √s(s - a)(s - b)(s - c)
where s = (a + b + c)/2.
Area of Square
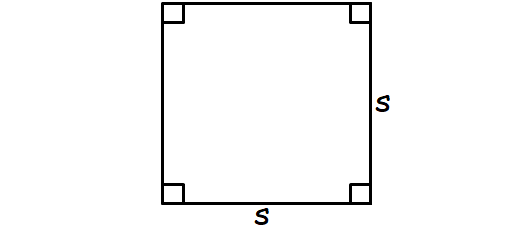
A plane figure with four equal straight sides and four right angles.
Formula for area of a square :
= s2
Area of Rectangle

A plane figure with four straight sides and four right angles, especially one with unequal adjacent sides, in contrast to a square.
Formula for area of a rectangle :
= length x width
or
= l x w
Area of Parallelogram
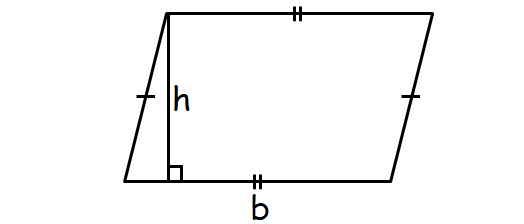
A parallelogram is a quadrilateral with opposite sides parallel.
Formula for area of a parallelogram :
= base x height
or
= b x h
Area of Rhombus
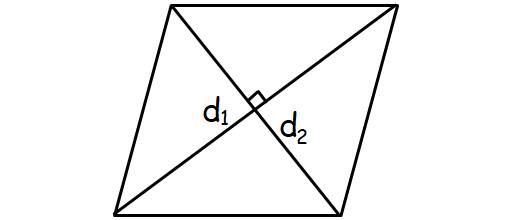
A rhombus is a parallelogram with four equal sides and equal opposite angles.
Formula for area of a rhombus :
= (1/2) x (d1 x d2)
Area of Quadrilateral
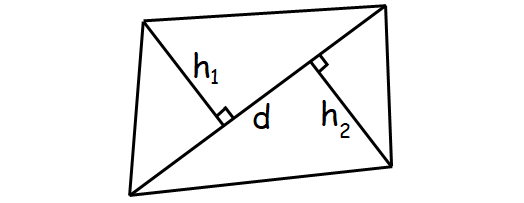
A shape which is having four sides is generally called quadrilateral.
Formula for area of a quadrilateral :
= (1/2) x d x (h1 + h2)
Area of Trapezoid
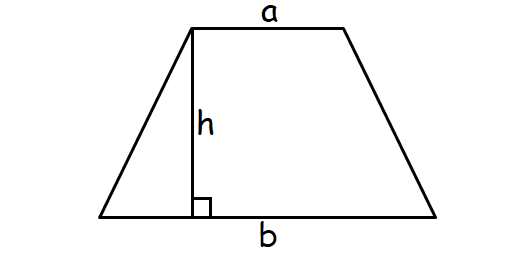
A quadrilateral with one pair of sides parallel.
Formula for area of a trapezoid :
= (1/2) x h(a + b)
Example 1 :
Find the area of the parallelogram.
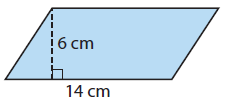
Solution :
Area of the parallelogram = b x h
Substitute b = 14 and h = 6.
= 14 x 6
= 84 cm2
Example 2 :
What is the area of a parallelogram that has a base of 12.75 in. and a height of 2.5 in.?
Solution :
Area of the parallelogram = b x h
Substitute b = 12.75 and h = 2.5.
= 12.75 x 2.5
= 31.875 in2
Example 3 :
Find the area of trapezoid.
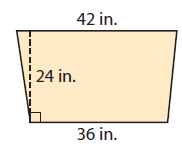
Solution :
Area of the trapezoid = (1/2) x h(a + b)
Substitute a = 42, b = 36 and h = 24.
= (1/2) x 24(36 + 42)
= 12 x 78
= 936 in2
Example 4 :
The bases of a trapezoid are 11 meters and 14 meters. If its height is 10 meters, find the area.
Solution :
Area of the trapezoid = (1/2) x h(a + b)
Substitute a = 11, b = 14 and h = 10.
= (1/2) x 10(11 + 14)
= 5 x 25
= 125 m2
Example 5 :
The diagonals of a rhombus are 21 m and 32 m. What is the area of the rhombus?
Solution :
Area of rhombus = (1/2) x (d1 x d2)
Subtract d1 = 21 and d2 = 32.
= (1/2) x (21 x 32)
= 21 x 16
= 336 m2
Example 6 :
Find the area of the given figure. Explain how you found your answer.
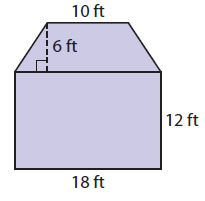
Solution :
In the given figure we can find two shapes, trapezoid and rectangle.
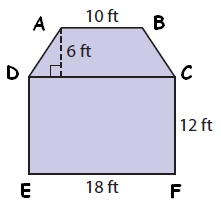
ABCD is a trapezoid, DCEF is a rectangle.
Area of the given figure :
= Area of trapezoid + Area of rectangle
Area of trapezoid :
= (1/2) x h(a + b)
Substitute a = 10, b = 18 and h = 6
= (1/2) x 6(10 + 18)
= 3 x 28
= 84 ft2
Area of rectangle DCEF :
= l x w
Substitute l = 18 and w = 12.
= 18 x 12
= 216 ft2
Area of the given figure :
= 84 + 216
= 300 ft2
Example 6 :
In the diagram below, MATH is a rectangle, GB = 4.6, MH = 6, and HT = 15.
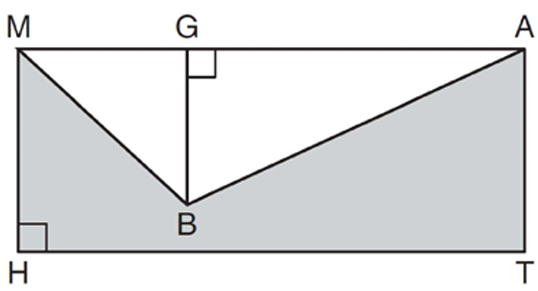
What is the area of polygon MBATH?
1) 34.5 2) 55.5 3) 90.0 4) 124.5
Solution :
To find the area of the shaded region, from the area of the rectangle we should subtract area of right triangles inside the rectangle.
= Area of rectangle - area of unshaded region
= HT x MH - (1/2) GB x MA
= 15 x 6 - (1/2) x 4.6 x 15
= 90 - 2.3 x 15
= 90 - 34.5
= 55.5
So, option (2) is the correct answer.
Example 7 :
A countertop for a kitchen is modeled with the dimensions shown below. An 18-inch by 21-inch rectangle will be removed for the installation of the sink.
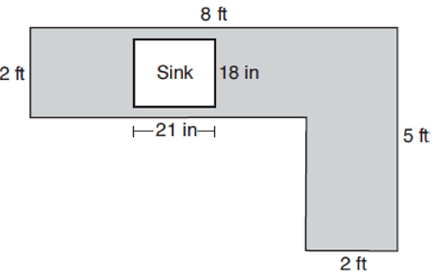
What is the area of the top of the installed countertop, to the nearest square foot?
1) 26 2) 22 3) 23 4) 19
Solution :
1 ft = 12 inches
1 inch = 1/12 ft
18 inches = 18/12
= 1.5 ft
21 inches = 21/12
= 1.75 inches
Area of countertop = 8 x 2 + 3 x 2 - (1.5 x 1.75)
= 16 + 6 - 2.625
= 22 - 2.625
= 19.375
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 47)
Mar 05, 26 09:19 PM
Digital SAT Math Problems and Solutions (Part - 47) -
Digital SAT Math Problems and Solutions (Part - 46)
Mar 05, 26 08:37 PM
Digital SAT Math Problems and Solutions (Part - 46) -
Digital SAT Math Problems and Solutions (Part - 45)
Mar 05, 26 08:02 PM
Digital SAT Math Problems and Solutions (Part - 45)