AREA AND PERIMETER OF A SQUARE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Area of a Square :
Area of a square is defined as the space occupied by the square shaped object on a flat surface. The area of a square can be measured by comparing the shape to squares of a fixed size.
Perimeter of a Square :
Perimeter of a square is a path that surrounds the square. The term may be used either for the path or its length it can be thought of as the length of the outline of a square.
In this section, you will learn how to find perimeter and area of square.
A square is a four-sided closed figure where the lengths of all the four sides will be equal and each vertex angle will be right angle or 90o as shown below.
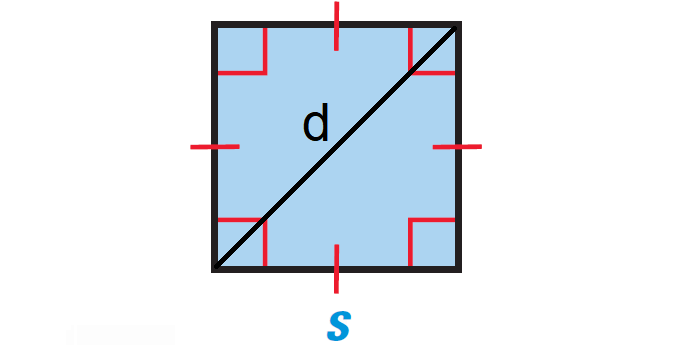
Formula for Area of a Square
The amount of space available inside the boundary of a two-dimensional space is called area.
We can use the following two formulas to calculate the amount of space available inside the square.
If s be the length of each side of a square, then the formula for area of a square :
Area = s2
If d be the length of each diagonal of a square, then, the formula for area of a square :
Area = ½ ⋅ d2
Formula for Perimeter of a Square
The distance around a two dimensional shape is called perimeter.
If s be the length of each side of a square, then the perimeter of the square is
= s + s + s + s
= 4s
So, the formula for perimeter of a square :
Perimeter = 4s
The measurements of perimeter and circumference use units such as centimeters, meters, kilometers, inches, feet, yards, and miles. The measurements of area use units such as square centimeters (cm2), square meters(m2), and so on.
Example 1 :
Find the perimeter and area of a square with side 7 cm.
Solution :
Perimeter :
= 4s
Substitute s = 7.
= 4 x 7
= 28 cm
Area :
= s2
Substitute s = 7.
= 72
= 7 x 7
= 49 cm2
Example 2 :
Find the perimeter and area of the square shown below.
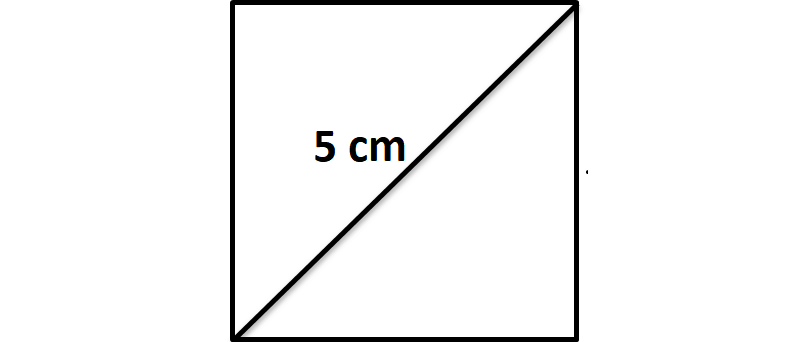
Solution :
To find the perimeter and area of square, we have to know the length of side of the square.
To find the length of side of the square, let us consider the right triangle in the given square as shown below.
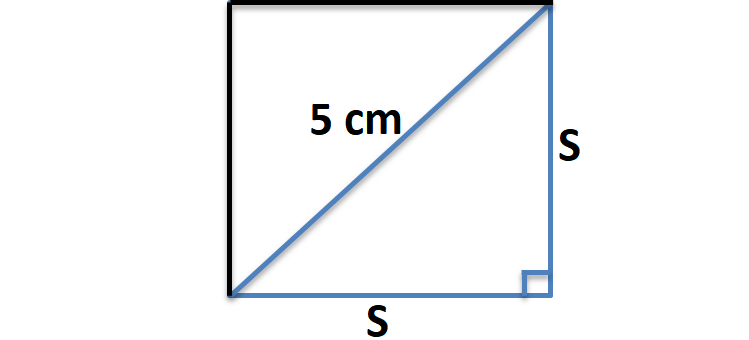
Use Pythagorean theorem to find the length of side of the square.
s2 + s2 = 52
2s2 = 25
Divide both sides by 2.
s2 = 25/2
s2 = 12.5
Take radical on both sides.
√s2 = √12.5
s = √12.5
Perimeter :
= 4s
Substitute s = √12.5.
= 4√12.5 cm
Area :
= s2
Substitute s = √12.5.
= (√12.5)2
= 12.5 cm2
Example 3 :
The area of a square is 32 square inches. Find the length of its diagonal.
Solution :
Area of the square = 32 in2
1/2 ⋅ d2 = 32
Multiply each side by 2.
d2 = 64
Find positive square root on both sides.
√d2 = √(8 ⋅ 8)
d = 8
So, the length of diagonal is 8 inches.
Example 4 :
The square has side length 36 inches. Find its area in square feet.
Solution :
When the length of a side is given, formula for area of a square :
= s2
Substitute 12 for s.
= 362
= 1296 in2 -----(1)
We know
12 inches = 1 ft
Square both sides.
(12 inches)2 = (1 ft)2
122 in2 = 12 ft2
144 in2 = 1 ft2
Therefore, to convert square inches into meter square feet, we have to divide by 144.
(1)-----> Area of the square = 1296 in2
Divide the right side by 144 to convert in2 into ft2.
Area of the square = (1296 / 144) ft2
= 9 ft2
So, the area of the square is 9 square feet.
Example 5 :
The diagonals of two squares are in the ratio 2 : 5. Find the ratio of their areas.
Solution :
Let the diagonals of two squares be 2x and 5x respectively.
Area of a square when diagonal is given :
= (½)d2
Area of first square = (1/2)(2x)2
= (½)(4x2)
= 2x2
Area of second square = (½)(5x)2
= (½)(25x2)
= 25x2/2
Ratio of their areas is
= 2x2 : 25x2/2
= 4x2 : 25x2
= 4 : 25
Note :
When the ratio of lengths of sides of two squares is given, to find the ratio of their areas, we have to square the lengths of sides and take ratio.
Example 6 :
A square is of area 64 cm2. What is its perimeter ?
Solution :
Area of a square = 64 cm2
s2 = 64
Take square root on both sides.
s = √64
s = 8 cm
Perimeter of the square :
= 4s
Substitute s = 8.
= 4(8)
= 32 cm
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
