ARCS AND CHORDS

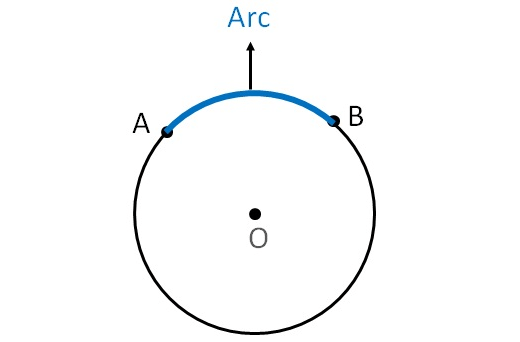
Arc - Definition :

The arc of a circle is a portion of the circumference of a circle.

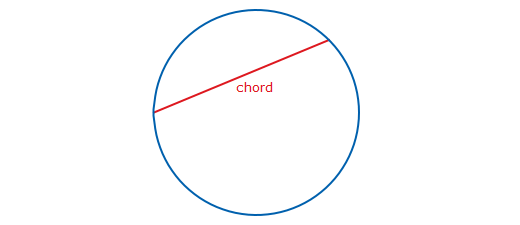
Chord - Definition :

A chord of a circle is a straight line segment whose endpoints both lie on the circle.

Using Arcs of Circles

In a plane, an angle whose vertex is the center of a circle is a central angle of the circle. 

If the measure of a central angle, ∠APB is less than 180°, then A and B and the points of circle ⊙P shown below in the interior of ∠APB form a minor arc of the circle. The points A and B and the points of the circle ⊙P in the exterior of ∠APB form a major arc of the circle. If the end points of an arc are the end points of a diameter, then the arc is a semicircle.      

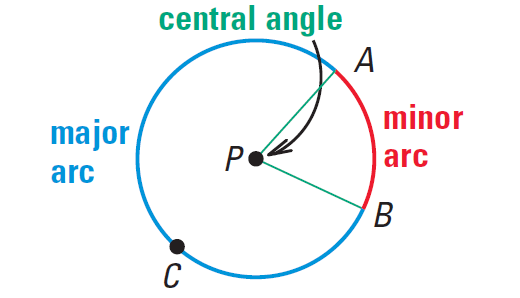
Naming Arcs

Arcs are named by their end points. For example, the minor arc associated with ∠APB above is AB. Major arcs and semicircles are named by their endpoints and by a point on the arc.

For example, the major arc associated with ∠APB above is ACB.

EGF below is a semicircle. 

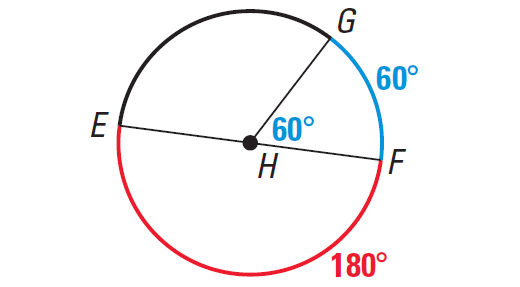
Measuring Arcs

The measure of a minor arc is defined to be the measure of its central angle.

For instant, in the above diagram, 

measure of arc GF  =  m∠GHF  =  60°

We can write the measure of an arc next to the arc. The measure of a semicircle is 180°. 

The measure of a major arc is defined as the difference between 360° and the measure of its associated minor arc.

For instant, in the above diagram, 

measure of arc GEF  =  360° - 60°  =  300°

The measure of a whole circle is 360°. 

Arc Addition Postulate

The measure of an arc formed by two adjacent arcs is the sum of the measures of the two arcs. 

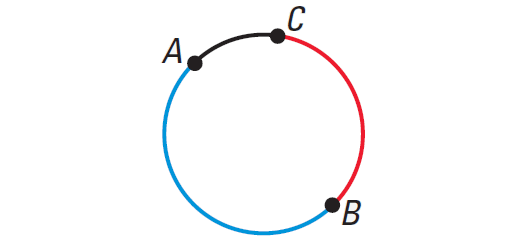
In the diagram shown above, we have

Theorems About Chords of Circles

Theorem 1 :

In the same circle or in congruent circles, two minor arcs are congruent, if and only if their corresponding chords are congruent.

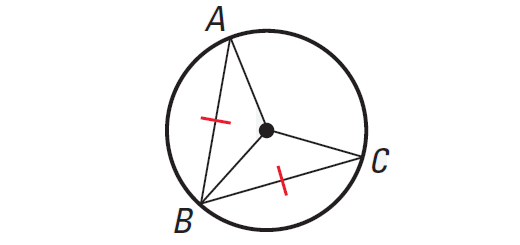
In the diagram shown above, we have

Theorem 2 :

If a diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc. 

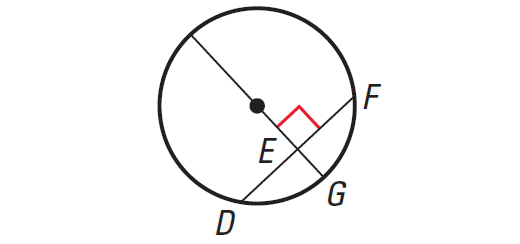
In the diagram shown above, we have

Theorem 3 :

If one chord is perpendicular bisector of another chord, then the first chord is a diameter. 

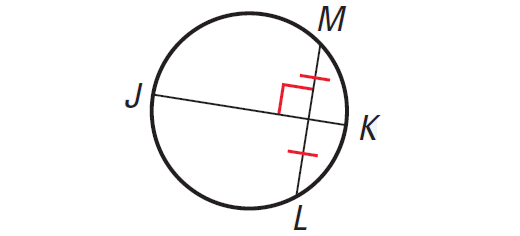
In the diagram shown above, chord JK is a perpendicular bisector of the chord ML.

So, chord JK is a diameter of the circle. 

Theorem 4 :

In the same circle or in congruent circles, two chords are are congruent, if and only if they are equidistant from the center. 

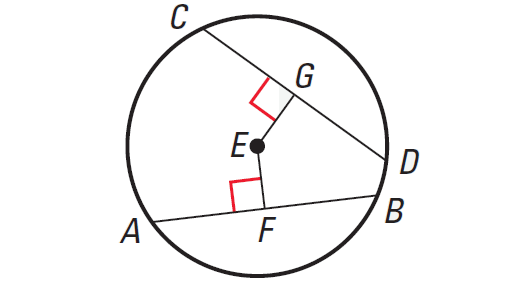
In the diagram shown above, we have

AB  ≅  CD, if and only if EF  ≅  EG

Finding Measures of Arcs

Example 1 :

Find the measure of arc MPN of ⊙R. 

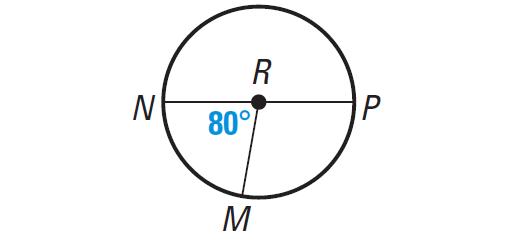
Solution :

Arc MPN is a major arc, so 

measure of arc MPN  =  360° - 80°

measure of arc MPN  =  280°

Identifying Congruent Arcs

Two arcs of the same circle or of congruent circles are congruent arcs, if they have the same measure. So, two minor arcs of the same circle or of congruent circles are congruent if their central angles are congruent. 

It has been illustrated in the following examples. 

Example 2 :

Find the measures of the blue arcs in the diagram shown below. Are they congruent ?

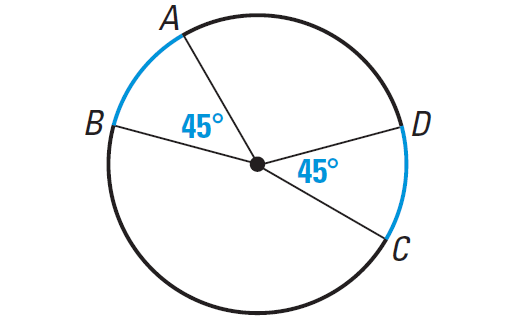
Solution :

Arcs AB and DC are in the same circle. 

And, m∠arc AB  =  m∠arc DC  =  45°. So, we have

arc AB  ≅  arc DC

Example 3 :

Find the measures of the blue arcs in the diagram shown below. Are they congruent ?

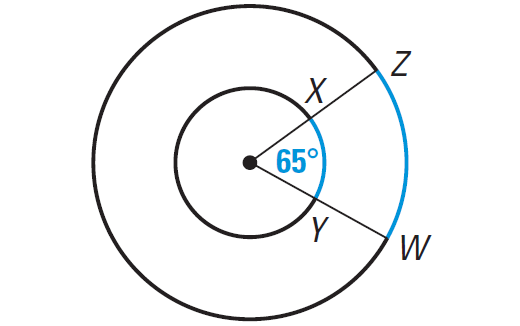
Solution :

m∠arc XY  =  m∠arc ZW  =  65°, but arc XY and arc ZW are not arcs of the same circle or of congruent circles. 

So, arc XY and arc ZW are not congruent. 

Using Properties of Chords 

Example 4 : 

A masonry hammer has a hammer on one end and a curved pick on the other end. The pick works best, if we swing it along a circular curve that matches the shape of the pick. Find the center of the circular swing.  

Solution :

Draw a segment AB, from the top of the masonry hammer to the end of the pick as shown in the diagram below. Find the midpoint C, and draw a perpendicular bisector CD. Find the intersection of CD with the line formed by the handle. 

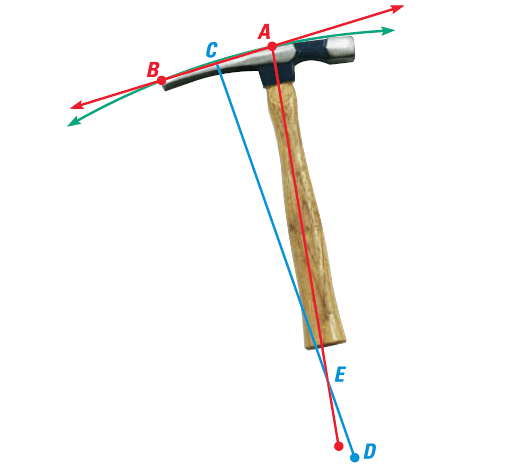
The point of intersection of CD with the line formed by the handle is the center of the swing. 

So, the center of the swing lies at E. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.