ARC LENGTH OF A SECTOR

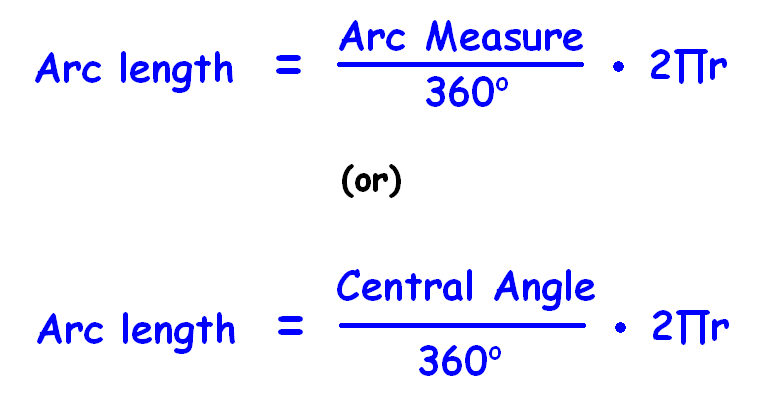
Formula to find the arc length of a sector is 

Example 1 :

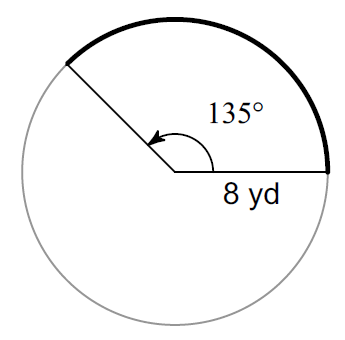
Find the length of the arc that is bolded. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

Solution :

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  8, Arc Measure  =  135° and Π  ≈  3.14

≈  (135° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 8

≈  18.9

So, the length of the arc is about 18.9 yd.

Example 2 :

Find the length of the arc that is bolded. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

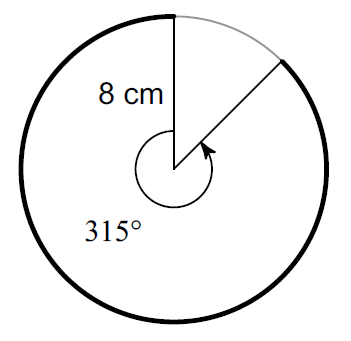
Solution :

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  8, Arc Measure  =  315° and Π  ≈  3.14

≈  (315° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 8

≈  44

So, the length of the arc is about 44 cm.

Example 3 :

Find the length of the arc highlighted in red color. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

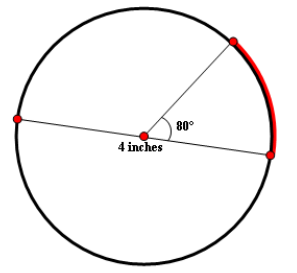
Solution :

Given : Diameter is 4 inches.

Then, the radius is

=  Diameter / 2

=  4 / 2

=  2 inches

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  2, Arc Measure  =  80° and Π  ≈  3.14

≈  (80° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 2

≈  2.8

So, the length of the arc is about 2.8 inches.

Example 4 :

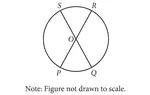
In the diagram given below, if QRS is a central angle and m∠QRS = 81°, m∠SRT = 115°, and radius is 5 cm, then find the length of the arc QST. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

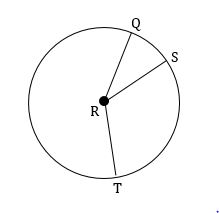
Solution :

To find the length of the arc QST, first we have to find the arc measure QST or the central angle m∠QRT. 

m∠QRT  =  m∠QRS + m∠SRT

m∠QRT  =  81° + 115°

m∠QRT  =  196°

The formula to find the arc length is

=  (Central Angle / 360°) ⋅ 2Π r

Plug r  =  5, Central Angle  =  196° and Π  ≈  3.14

≈  (196° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 5

≈  17.1

So, the length of the arc is about 17.1 cm.

Example 5 :

If m∠LMN = 19° and radius is 15 inches, then find the length of arc LN. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

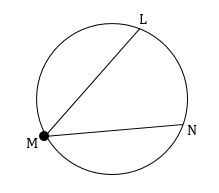
Solution :

To find the length of the arc LN, first we have to find the arc measure LN. 

By Inscribed Angle Theorem, we have

1/2 ⋅ Arc Measure  =  m∠LMN

Multiply both sides by 2. 

Arc Measure  =  2 ⋅ m∠LMN

Arc Measure  =  2 ⋅ 19°

Arc Measure  =  38°

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  15, Arc Measure  =  38° and Π  ≈  3.14

≈  (38° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 15

≈  9.9

So, the length of the arc is about 9.9 inches.

Example 6 :

In a circle, if the arc length of Arc AB is 18 cm and the measure of Arc AB is 39°, then find the radius of the circle. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary) 

Solution :

Given : The arc length of Arc AB is 18 cm.

So, we have

(Arc Measure / 360°) ⋅ 2Π r  =  18

Plug Arc Measure  =  39° and Π  ≈  3.14

(39° / 360°) ⋅ 2 ⋅ 3.14 ⋅ r  ≈  18  

(39° / 360°) ⋅ 2 ⋅ 3.14 ⋅ r  ≈  18

0.1083 ⋅ 2 ⋅ 3.14 ⋅ r  ≈  18

0.68 ⋅ r  ≈  18

Divide both sides by 0.68. 

r  ≈  18 / 0.68

r  ≈  26.5

So, the radius of the circle is about 26.5 cm.

Example 7 :

In a circle, if the arc length of Arc AB is 19 inches and the radius is 29 inches, then find the measure of arc AB. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary) 

Solution :

Given : The arc length of Arc AB is 19 inches.

So, we have

(Arc Measure / 360°) ⋅ 2Π r  =  19

Plug r  =  29 and Π  ≈  3.14

(Arc Measure / 360°) ⋅ 2 ⋅ 3.14 ⋅ 29  ≈  19 

(Arc Measure / 360°) ⋅ 182.12  ≈  19

(Arc Measure / 360°) ⋅ 182.12  ≈  19

Multiply both sides by 360° / 182.12

Arc Measure  ≈  19 ⋅ 360° / 182.12

Arc Measure  ≈  19 ⋅ 360° / 182.12

Arc Measure  ≈  37.6°

So, the measure of arc AB is about 37.6°.

Example 8 :

Find the length of the arc highlighted in red color. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

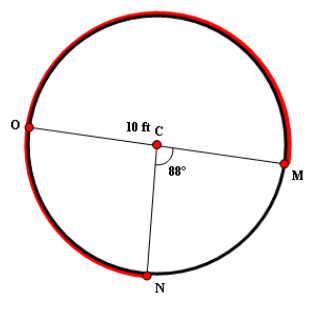
Solution :

From the given diagram, we have

m∠MCN + Measure of arc MON  =  360°

Plug m∠MCN  =  88°

88° + Measure of arc MON  =  360°

Subtract 88° from both sides. 

Measure of arc MON  =  272°

Given : Diameter is 4 inches.

Then, the radius is

=  Diameter / 2

=  10 / 2

=  5 ft

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  5, Arc Measure  =  272° and Π  ≈  3.14

≈  (272° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 5

≈  23.7 ft

So, the length of the arc is about 23.7 ft.

Example 9 :

A lasso is made from a rope that is 10 m long. The loop of the lasso has a radius 0.6 m when circular. Find the length of the rope that is not part of the loop.

Solution :

Length of rope which is aligned in a line + circumference of circular loop = 10 m

l + 2Π r = 10

Here r = 0.6 m

l + 2(3.14) (0.6) = 10

l + 3.768 = 10

l = 10 - 3.768

l = 6.232 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.