ARC AND ANGLE RELATIONSHIPS IN CIRCLES WORKSHEET

Problem 1 :

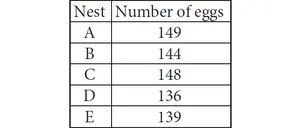
Find m∠AED. 

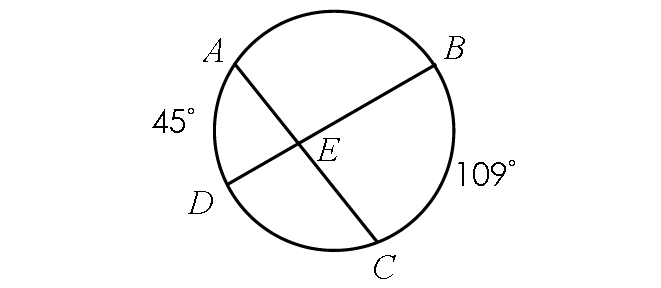
Problem 2 :

Find m∠YWX. 

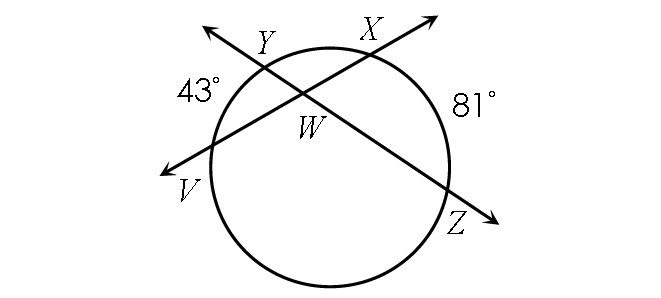
Problem 3 :

Find m∠arc CDE. 

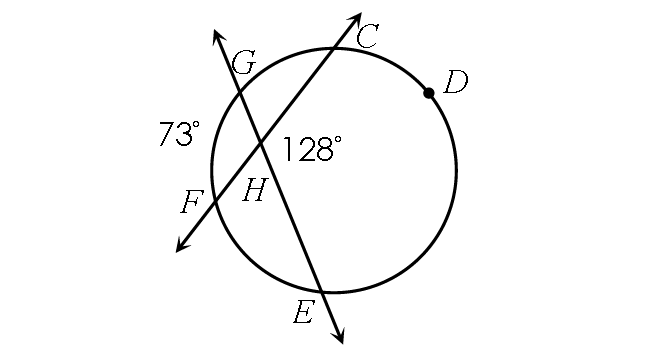
Problem 4 :

Find m∠DEG. 

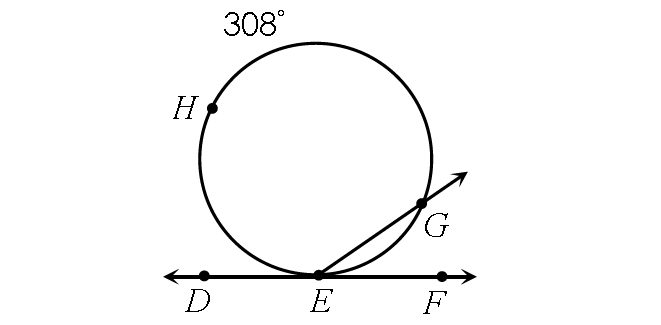
Problem 5 :

Find m∠arc KNM. 

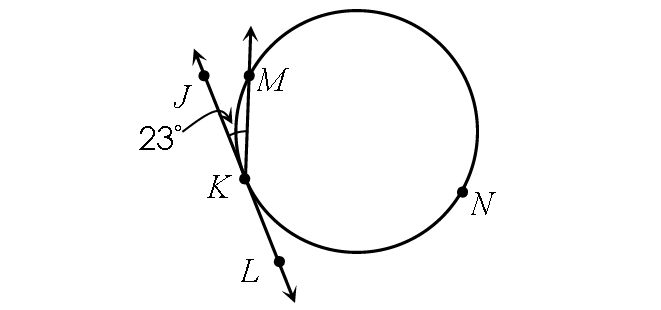
Problem 6 :

Find m∠KLM. 

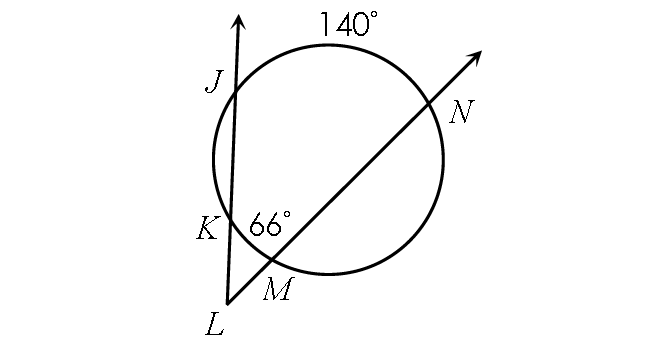
Problem 7 :

Find m∠BCD. 

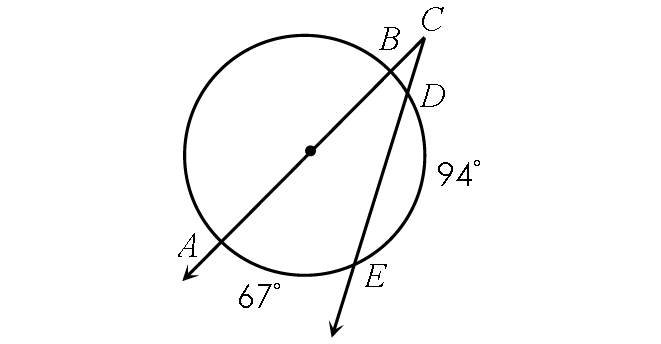
Problem 8 :

Find m∠KLM. 

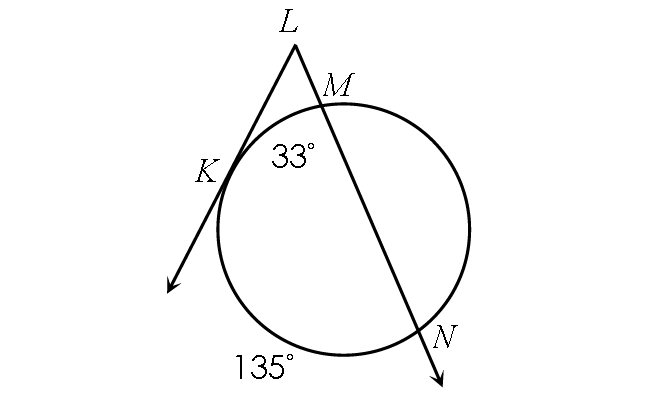
Problem 9 :

Find m∠CDE. 

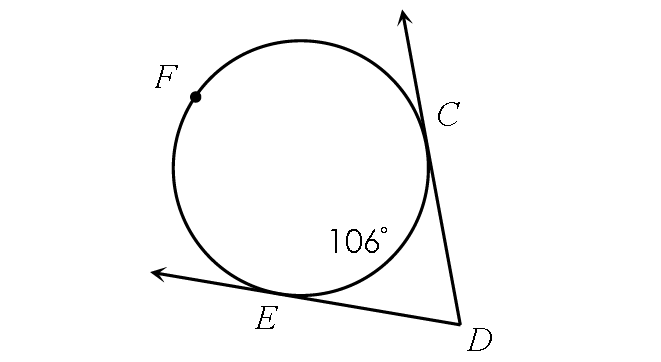
Problem 10 :

Find m∠arc MK. 

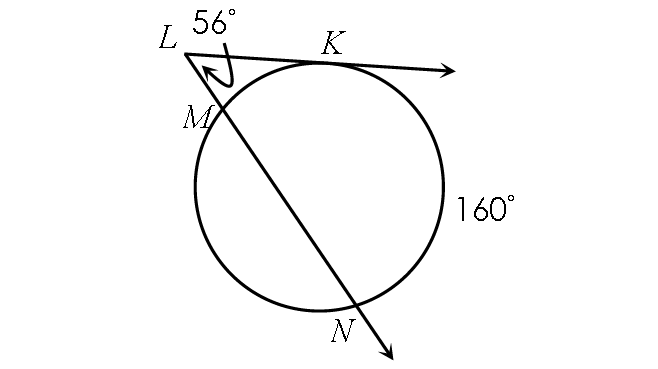
Answers

1. Answer :

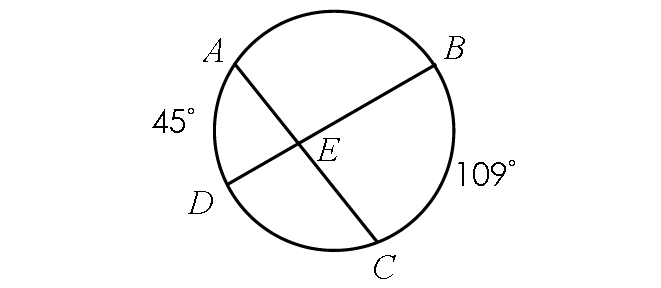
m∠AED = ½ ⋅ (m∠arc AD + m∠arc BC)

Substitute. 

m∠AED = ½ ⋅ (45° + 109°)

m∠AED = ½ ⋅ 154°

m∠AED = 77°

2. Answer :

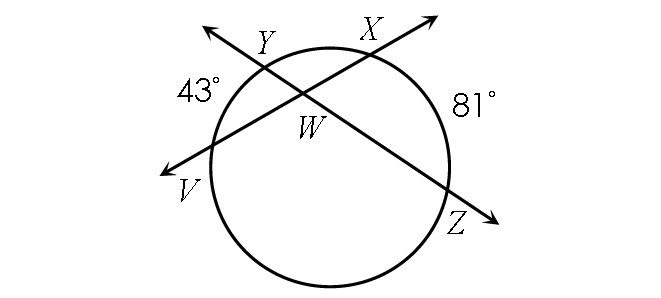
Find m∠VWY : 

 m∠VWY = ½ ⋅ (m∠arc VY + m∠arc XZ)

m∠VWY = ½ ⋅ (43° + 81°)

m∠VWY = ½ ⋅ 124°

m∠VWY = 62°

Find m∠YWX :

m∠VWY and m∠YWX are linear pair. 

Then, 

m∠VWY + m∠YWX = 180°

Substitute m∠VWY = 62°. 

62° + m∠YWX = 180°

Subtract 62° from each side. 

m∠YWX = 118°

3. Answer :

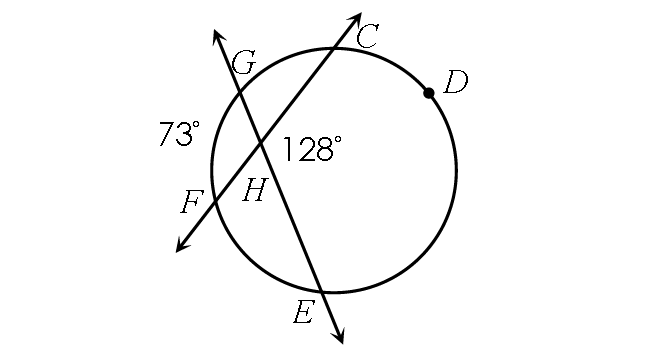
½ ⋅ (m∠arc GF + m∠arc CDE) = m∠CHE

Substitute. 

½ ⋅ (73° + m∠arc CDE) = 128°

Multiply each side by 2.

73° + m∠arc CDE = 256°

Subtract 73° from each side. 

m∠arc CDE = 183°

4. Answer :

m∠DEG = ½ ⋅ m∠arc EHG

Substitute. 

m∠DEG = ½ ⋅ 308°

m∠DEG = 154°

5. Answer :

Find m∠arc KM :

½ ⋅ m∠arc KM = m∠JKM

Substitute. 

½ ⋅ m∠arc KM = 23°

Multiply each side by 2. 

m∠arc KM = 46°

In the circle above,

m∠arc KM + m∠arc KNM = 360°

Substitute. 

46° + m∠arc KNM  =  360°

Subtract 46° from each side.

m∠arc KNM = 314°

6. Answer :

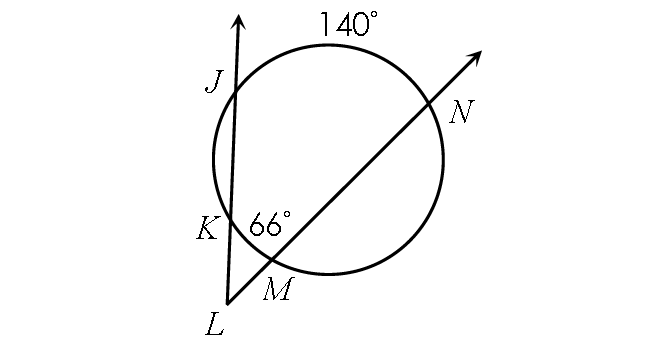
m∠KLM = ½ ⋅ (m∠arc JN - m∠arc KM)

Substitute. 

m∠KLM = ½ ⋅ (140° - 66°)

m∠KLM = ½ ⋅ 74°

m∠KLM = 37°

7. Answer :

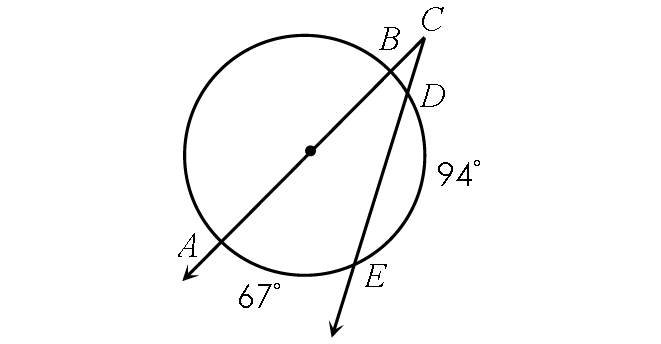
In the circle above,

m∠arc BD + m∠arc DE + m∠arc EA = 180°

Substitute. 

m∠arc BD + 94° + 67° = 180°

m∠arc BD + 161° = 180°

Subtract 161° from each side. 

m∠arc BD = 19°

Finding m∠BCD : 

  m∠BCD = ½ ⋅ (m∠arc AE - m∠arc BD)

Substitute. 

m∠BCD = ½ ⋅ (67° - 19°)

m∠BCD = ½ ⋅ 48°

m∠BCD = 24°

8. Answer :

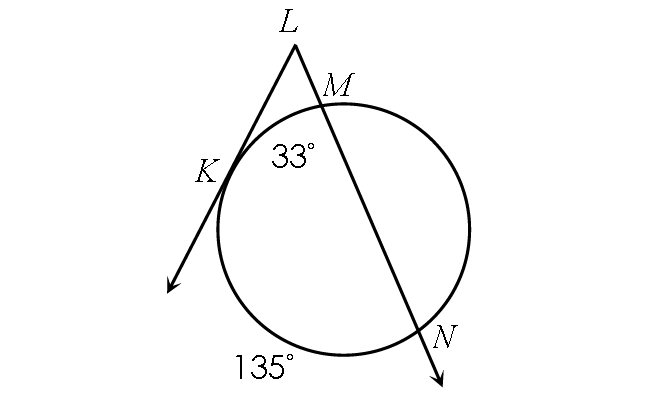
m∠KLM = ½ ⋅ (m∠arc KN - m∠arc KM)

Substitute. 

m∠KLM = ½ ⋅ (135° - 33°)

m∠KLM = ½ ⋅ 102°

m∠KLM = 51°

9. Answer :

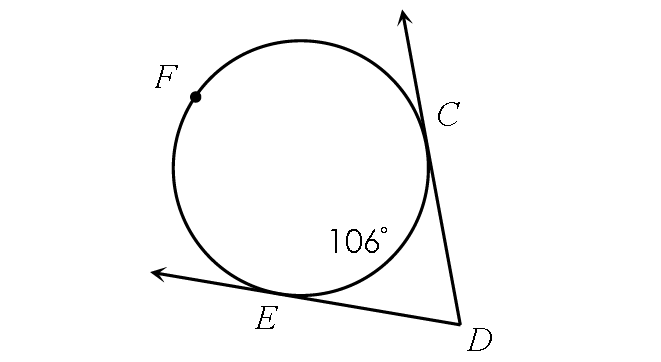
In the circle above,

m∠arc CFE + m∠arc CE = 360°

Substitute. 

m∠arc CFE + 106° = 360°

Substitute 106° from each side. 

m∠arc CFE = 254°

Finding m∠CDE : 

m∠CDE = ½ ⋅ (m∠arc CFE - m∠arc CE)

Substitute. 

m∠CDE = ½ ⋅ (254° - 106°)

m∠KLM = ½ ⋅ 148°

m∠KLM = 74°

10. Answer :

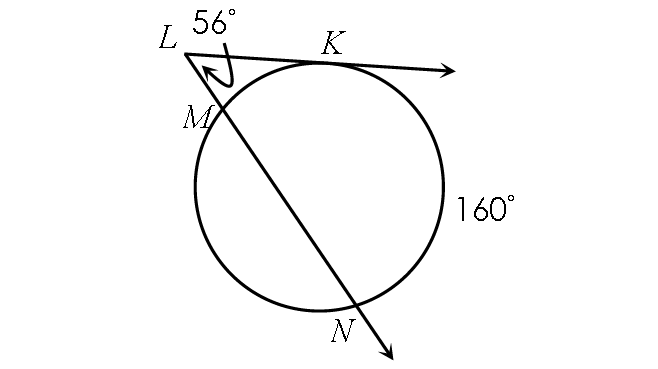
½ ⋅ (m∠arc NK - m∠arc MK) = m∠MLK

Substitute. 

½ ⋅ (160° - m∠arc MK) = 56°

Multiply each side by 2. 

160° - m∠arc MK = 112°

Subtract 160° from each side.  

- m∠arc MK = -48°

Multiply each side by -1. 

m∠arc MK = 48°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.