APPROXIMATING AREA UNDER A CURVE WITH RECTANGLES

Find the area of the region S that  lies under the curve y  f(x) from a to b.

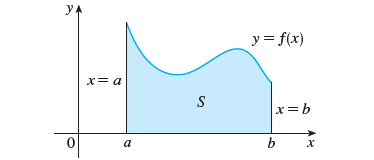
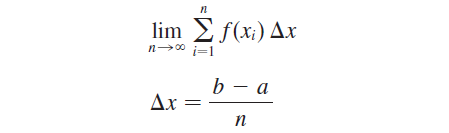
We approximate the region S by rectangles and then we take limit of the areas of these rectangles as we increase the number of rectangles. The following example illustrates the procedure.

Example 1 :

Use rectangles to estimate the area under the parabola y = x² from 0 to 1.

Solution :

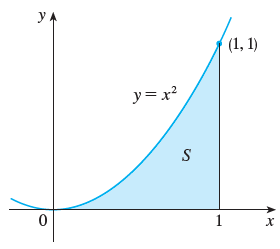
We first notice that area S must be somewhere between 0 and 1 because S is contained. Suppose we divide S into four strips S₁, S₂, S₃ and S₄ by drawing vertical lines x.

Δx  =  (1 - 0)/4

Δx  =  1/4

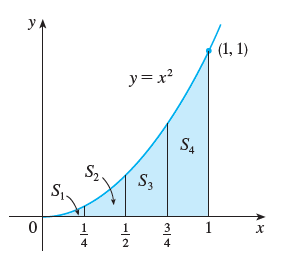
We can approximate each strip by that has the same base as the strip and whose height is the same as the right edge of the strip. Each rectangle has the width of 1/4.

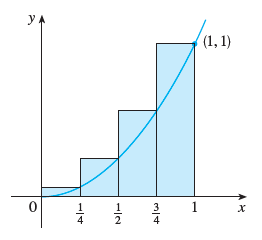
In other words the height of these rectangles of the function  y = x² at the right endpoints of the sub intervals [0, 1/4], [1/4, 1/2] [1/2, 3/4] and [3/4, 1]. 

Approximating area using right end points :

f(1/4)  =  (1/4)²  =  1/16

f(1/2)  =  (1/2)²  =  1/4

f(3/4)  =  (3/4)²  =  9/16

f(1)  =  1²  =  1

Required area  =   (1/4) [(1/16) + (1/4) + (9/16) + 1]

=  (1/4)((1+4+9+16)/16)

=  (1/4)(20/16)

=  0.25(1.25)

=  0.3125

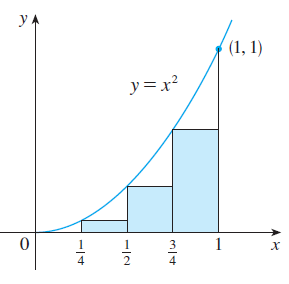
The function  y = x² at the left endpoints of the sub intervals [0, 1/4], [1/4, 1/2] [1/2, 3/4] and [3/4, 1]. 

Approximating area using left end points :

f(0)  =  0²  =  0

f(1/4)  =  (1/4)²  =  1/16

f(1/2)  =  (1/2)²  =  1/4

f(3/4)  =  (3/4)²  =  9/16

Required area  =   (1/4) [0 + (1/16) + (1/4) + (9/16)]

=  (1/4)((0+1+4+9)/16)

=  (1/4)(14/16)

=  0.25(0.875)

=  0.21875

So, the area of S is larger than area.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.