APPLYING MULTIPLICATION AND DIVISION OF RATIONAL NUMBERS

Applying Multiplication and Division of Rational Numbers :

To solve many problems in math, often we may have to use multiplication and division of rational numbers. 

In this section, we are going to learn how to multiply and divide rational numbers. 

Note : 

Rational numbers are usually denoted in the form "a/b".

That is, fraction form.

Multiplying Fractions

Stuff 1 :

To multiply a proper or improper fraction by another proper or improper fraction, we have to multiply the numerators and denominators. 

For example, 

2/3 x 4/5   =  8/15

1/3 x  7/11  =  7/33

Stuff 2 :

To multiply a proper or improper fraction by a whole number, we have to multiply the numerator of the fraction by the whole number. 

For example, 

(2/3) x 4   =  8/3

3 x  7/11  =  21/33

Multiplying Fractions - Examples

Example 1 :

Find 1/5 of 3/8

Solution : 

1/5 of 3/8  =  1/5 x 3/8

1/5 of 3/8  =  3/40

Example 2 :

Find 2/9 x 3/2

Solution : 

2/9 x 3/2  =  1/3

Example 3 :

Find 2/5 x 5 2/3

Solution : 

2/5 x 5 2/3  =  2/5 x 17/3

2/5 x 5 2/3  =  34/15

2/5 x 5 2/3  =  2 4/15 

Example 4 :

Find 6 3/4 x 7/10

Solution : 

6 3/4 x 7/10  =  27/4 x 7/10

6 3/4 x 7/10  =  (27x7) / (4x10)

6 3/4 x 7/10  =  189 / 40

6 3/4 x 7/10  =  4 29/40

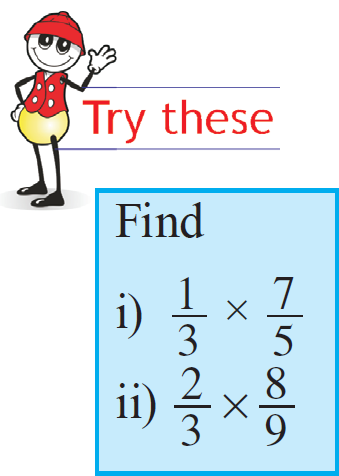
Example 5 :

Lily reads 1/4 th of a book in 1 hour. How much of the book will she read in 3 1/2 hours ?

Solution : 

The part of the book read by Lily in 1 hour  =  1/4  

So, the part of the book read by Lily in 3 1/2 hours is

=  3 1/2 x 1/4

=  7/2 x 1/4

=  (7x1) / (2x4)

=  7/8

Hence, Lily reads 7/8 part of the book in 3 1/2 hours.

Example 6 :

David ate 1/3 of the pizza and gave 3/4 th of the remaining to his friend. What is the part of the pizza did David give his friend ?  

Solution : 

The part of the pizza eaten by David  =  1/3 

So, the remaining pizza  =  2/3

The part of the given to his friend is

=  3/4 of the remaining

=  3/4 of 2/3

=  3/4 x 2/3

=  1/2

Hence, he gave 1/2 of the pizza to his friend. 

Dividing Fractions

Step 1 :

When we divide a fraction by another fraction, first we have to change the division sign as multiplication.

Step 2 :

Take reciprocal of the second fraction.

Step 3 :

Multiply the two fractions. (Numerator times numerator and denominator times denominator).

Dividing Fractions - Examples

Example 1 : 

Simplify : 2/5 ÷  6/7 

Solution : 

Using the method explained above, we have 

 2/5 ÷ 6/7  =  2/5 x 7/6

2/5 ÷ 6/7  =  (2x7) / (5x6)

2/5 ÷ 6/7  =  7/15

Example 2 :

Simplify : 7/5 ÷ 3/2

Solution : 

Using the method explained above, we have 

7/5 ÷ 3/2  =  7/5 x 2/3

7/5 ÷ 3/2  =  (7x2) / (5x3)

7/5 ÷ 3/2  =  14/15

Example 3 :

Simplify : 5/12 ÷ 20/13

Solution : 

Using the method explained above, we have 

5/12 ÷ 20/13  =  5/12 ÷ 20/13

5/12 ÷ 20/13  =  5/12 x 13/20

5/12 ÷ 20/13  =  (5x13) /  (12x20)

5/12 ÷ 20/13  =  13/48

Example 4 :

Simplify : 2/19 ÷ 6 1/2

Solution : 

First, let us convert the mixed number 6 1/2 in to improper fraction.

6 1/2  =  13/2

Now,m we have 2/19 ÷ 6 1/2  =  2/19 ÷ 13/2

 Using the method explained above, we have 

2/19 ÷ 13/2 =  2/19 x 13//2

2/19 ÷ 13/2 =  (2x13) / (19x2)

2/19 ÷ 13/2 =  13 / 19

Example 5 :

David can make one pizza in 1/2 hour. How many pizzas can he make in 5/2 hours ?

Solution : 

Time taken to make one pizza  =  1/2 hour  

No. of pizzas made in 5/2 hours  =  5/2 ÷ 1/2

No. of pizzas made in 5/2 hours  =  5/2 x 2/1

No. of pizzas made in 5/2 hours  =  (5x2) / (2x1)

No. of pizzas made in 5/2 hours  =  5

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.