AP CALCULUS PRACTICE TEST

Problem 1 :

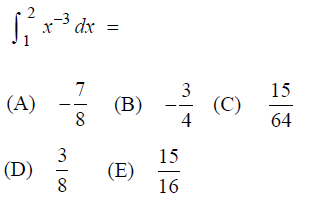
Solution :

Integrating x^-3, we get

=  x^(-3+1)/(-3+1)

=  -x^-2/2

Applying the upper and lower limits, we get

=  -(2^-2)/2 + (1^-2/2)

=  -1/8 + (1/2)

=  (-1+4)/8

=  3/8

Option D is correct.

Problem 2 :

Solution :

f(x)  =  (2x+1)⁴

f'(x)  =  4(2x+1)³ (2)  ==>  8(2x+1)³

f''(x)  = 48(2x+1)²

f'''(x)  = 192(2x+1)

f'^v(x)  = 384

Option E is correct.

Problem 3 :

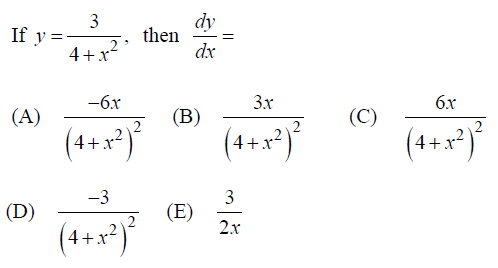
Solution :

y  =  3/(4+x²)

y  =  3(4+x²)^-1

dy/dx  =  -3(4+x²)^-2(2x)

dy/dx  =  -6x/(4+x²)²

Option A is correct.

Problem 4 :

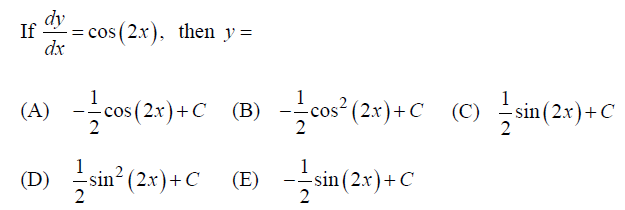
Solution :

dy/dx  =  cos 2x

∫dy/dx  =  cos 2x

Integrating on both sides, we get

y  =   sin2x/2 + C

Option C is correct.

Problem 5 :

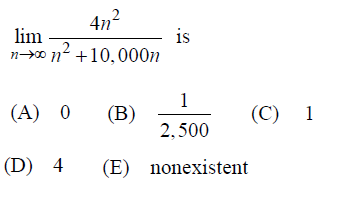
Solution :

=  lim n->∞   n²(4)/n²(1+10000/n)

=  lim n->∞ 4/(1+10000/n)

Applying the limit, we get

=  lim n->∞ 4/(1+10000/n)

=  4

So, option D is correct.

Problem 6 :

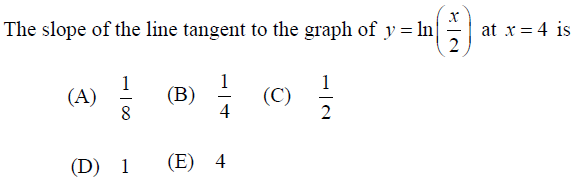
Solution :

y  =  ln(x/2)

Differentiating with respect to x, we get

dy/dx  =  [1/(x/2)] ⋅ (1/2)

dy/dx  =  1/x

Slope at x  =  4

dy/dx  =  1/4

Slope of the tangent at the point x = 4 is 1/4.

So, the correct option is B.

Problem 7 :

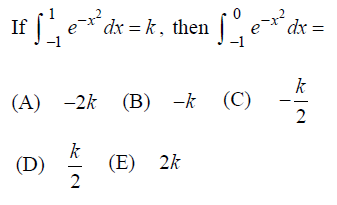
Solution :

Since the given function is even.

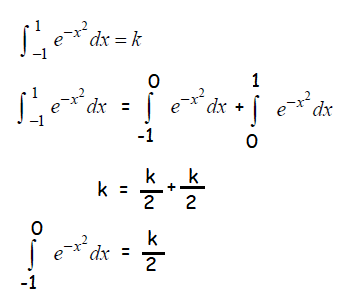
So, option D is correct.

Problem 8 :

Solution :

Given that,

s(t)  =  t²+4t+4

s'(t)  =  2t+4

a(t)  =  s''(t)  =  2

Acceleration is 2.

So, option B is correct.

Problem 9 :

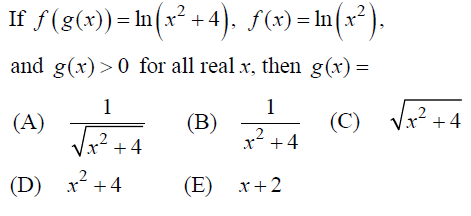
Solution :

Let g(x)  =  1/√(x²+4)

More clearly f(x)  =  ln(x²)

f(g(x))  =  ln(1/√(x²+4))²

It is not true. So, let us apply the next option.

Let g(x)  =  √(x²+4)

f(g(x))  =  ln(√(x²+4))²

f(g(x))  =  ln((x²+4)

It is true. 

So, option C is correct.

Problem 10 :

Solution :

f(x)  =  x³-3x²

f'(x)  =  3x²-6x

f'(x)  =  3x(x-2)

Using first derivative, let us find critical points.

f'(x)  =  0

3x(x-2)  =  0

x  =  0 and x  =  2

Note :

If the first derivative is negative to the left of the critical point and positive to the right of critical point, it has relative minimum at c.

If the first derivative is positive to the left of the critical point and negative to the right of critical point, it has relative maximum at c.

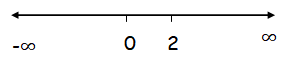
Let x  = -1  ∈ (-∞, 0)

f'(x)  =  3x(x-2)

f'(-1)  =  9 > 0 (positive)

Let x  = 1  ∈ (0, 2)

f'(x)  =  3x(x-2)

f'(1)  =  -3 < 0 (negative)

So, relative maximum at x  =  0.

Option B is correct.

Problem 11 :

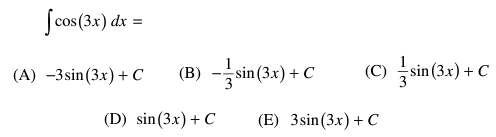
Solution :

∫ cos 3x dx 

Formula to be used,

∫ cos ax dx = (1/a) sin a x + C

∫ cos 3x dx = (1/3) sin 3x + C

So, option (C) is correct.

Problem 12 :

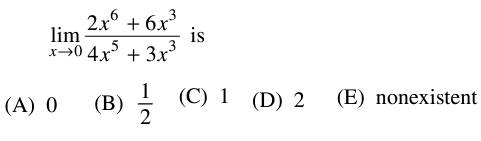
Solution :

= lim x--> 0 (2x⁶ + 6x³)/(4x⁵ + 3x³)

Factoring 2x³ from the numerator and factoring x³ from the denominator, we get

= lim x--> 0 (2x³ / x³) (x³ + 3)/(4x² + 3)

= lim x--> 0 { 2 (x³ + 3)/(4x² + 3) }

Applying the limit, we get

= 2(3) / 3

= 2

So, option D is correct.

Problem 13 :

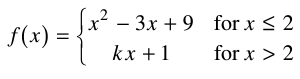
The function f is defined above, for what value of k if any is continuous at x = 2 ?

A)  1      B)  2      C)  3      D)  7

E) No value of k will make f continuous at x = 2.

Solution :

If the function is continuous at x = 2, then 

lim x--> 2^- and lim x--> 2⁺ will be equal.

lim x-->2^- f(x) = lim x-->2^- (x² - 3x + 9)

= 2² - 3(2) + 9

= 4 - 6 + 9

= 13 - 6

= 7-----(1)

lim x-->2⁺ f(x) = lim x-->2⁺ (kx + 1)

= k(2) + 1

= 2k + 1-----(2)

lim x-->2^- f(x) =lim x-->2⁺ f(x)

2x + 1 = 7

2x = 7 - 1

2x = 6

x = 6/2

x = 3

So, option (C) is correct.

Problem 14 :

If f(x) = cos³ (4x), then f'(x) = 

Solution :

f(x) = cos³ (4x)

f'(x) = 3 cos² (4x) (4)

= 12cos² (4x)

So, the value of f'(x) is 12cos² (4x).

Problem 15 :

The function f is given by f(x) = 2x³ - 3x² - 12x has a relative minimum at x = ?

Solution :

f(x) = 2x³ - 3x² - 12x

To find relative maximum or minimum at which point of x, we have to find the second derivative.

f'(x) = 2(3x²) - 3(2x) - 12(1)

= 6x² - 6x - 12

f'(x) = 0

6x² - 6x - 12 = 0

x² - x - 2 = 0

(x - 2)(x + 1) = 0

x = 2 and x = -1

Applying these two values in second derivative, we will get to know whether it has maximum or minimum.

f''(x) = 6(2x) - 6(1) - 0

= 12x - 6

f''(-1) = 12(-1) - 6

= -18 < 0 

Relative maximum at x = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.