ANGLES WORKSHEET

Question 1 :

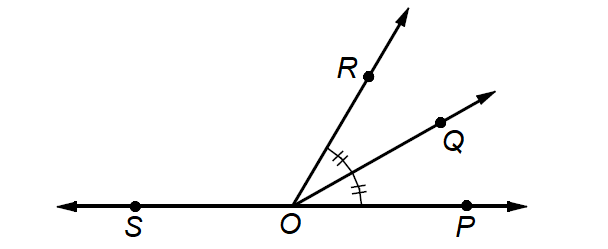
In the figure above, ray OQ bisects ∠ROP.

If ∠SOQ = 11x + 6 and ∠ROP = 8x - 12, what is the measure of ∠SOR?

A) 92

B) 96

C) 102

D) 108

Question 2 :

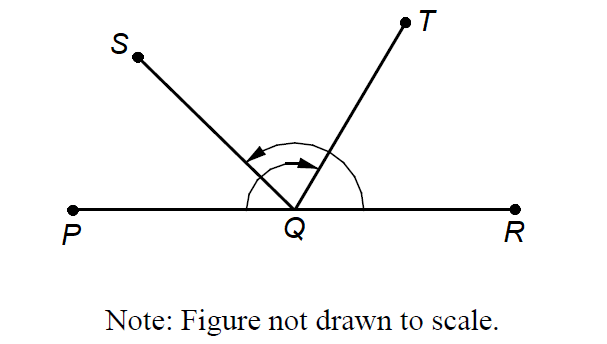
In the figure above, ∠PQT = 120° and ∠SQR = 135°. What is the measure ∠SQT?

A) 63

B) 68

C) 75

D) 79

Question 3 :

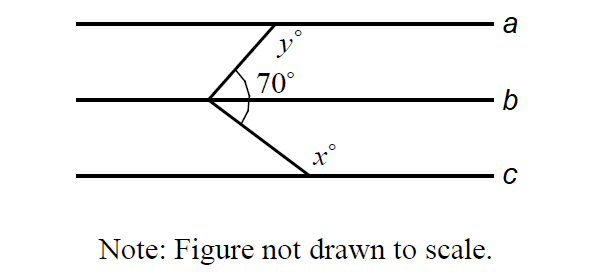
In the figure above, lines a, b and c are parallel. What is the value of (x + y)?

A) 160

B) 200

C) 230

D) 290

Question 4 :

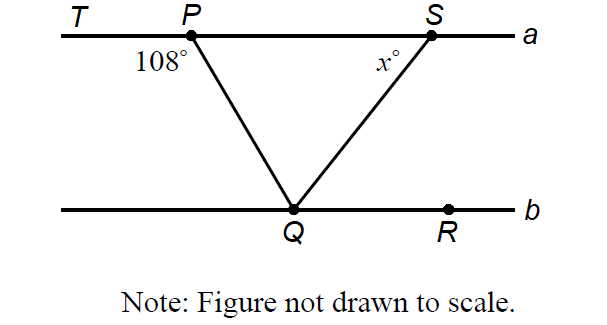
In the figure above, lines a and b are parallel and QS bisects ∠PQR. What is the value of x?

A) 54

B) 60

C) 68

D) 72

Question 5 :

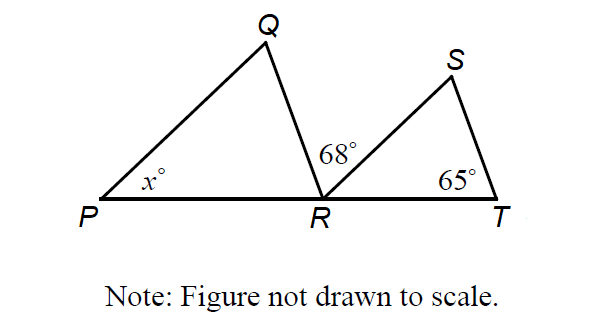
In the figure above, PQ || RS and QR || ST. What is the value of x?

A) 47

B) 51

C) 55

D) 57

Question 6 :

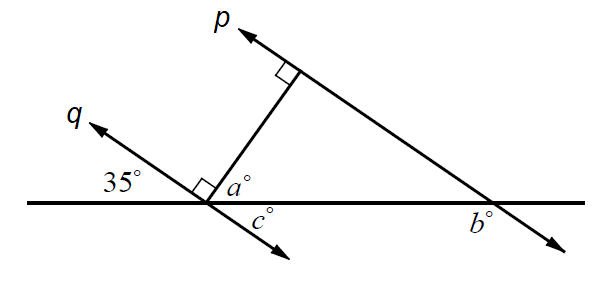
In the figure above, p || q. What is the value of (a + b)?

A) 160

B) 175

C) 185

D) 200

Question 7 :

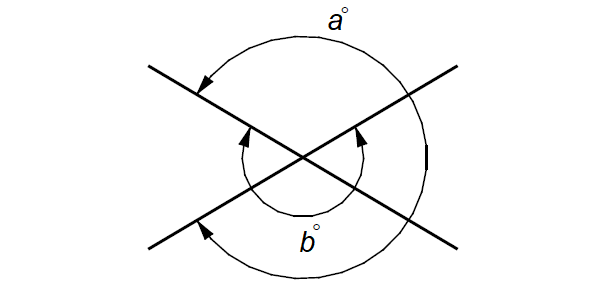
In the figure above, what is the value of (a + b)?

Question 8 :

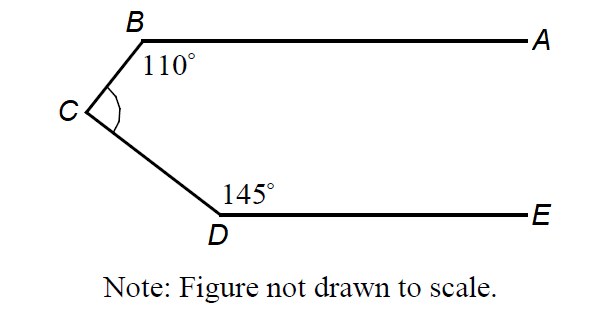
In the figure above, AB is parallel to DE. What is the measure of ∠BCD?

Question 1 :

In the figure above, ray OQ bisects ∠ROP.

If ∠SOQ = 11x + 6 and ∠ROP = 8x - 12, what is the measure of ∠SOR?

A) 92

B) 96

C) 102

D) 108

Answer :

Since ray OQ bisects ∠ROP,

∠QOP = (1/2)∠ROP

∠QOP = (1/2)(8x - 12)

∠QOP = 4x - 6

∠SOQ  and ∠QOP together form a linear pair.

∠SOQ + ∠QOP = 180°

11x + 6 + 4x - 6 = 180

15x = 180

x = 12

Given :

∠ROP = 8x - 12

Substitute x = 12.

∠ROP = 8(12) - 12

∠ROP = 96 - 12

∠ROP = 84°

∠SOR  and ∠ROP together form a linear pair.

∠SOR + ∠ROP = 180°

∠SOR + 84° = 180°

∠SOR = 96°

The correct answer choice is (A).

Question 2 :

In the figure above, ∠PQT = 120° and ∠SQR = 135°. What is the measure ∠SQT?

A) 63

B) 68

C) 75

D) 79

Answer :

Let ∠SQT = x.

∠PQS = ∠PQT - ∠SQT

∠PQS = 120° - x

In the figure above,

∠PQS + ∠SQR = 180°

120° - x + 135° = 180°

-x + 255 = 180°

-x = -75°

x = 75°

∠SQT = 75° 

The correct answer choice is (C).

Question 3 :

In the figure above, lines a, b and c are parallel. What is the value of (x + y)?

A) 160

B) 200

C) 230

D) 290

Answer :

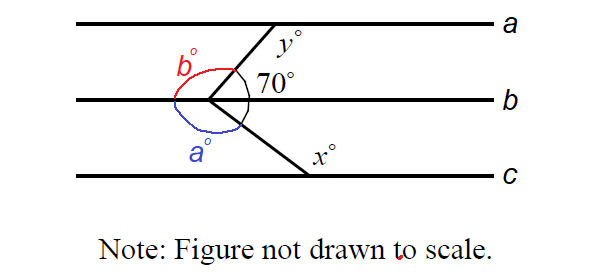
In the figure above,

a° + b° + 70° = 360°

a + b = 290 ----(1)

x° and a° are alternate interior angles and they are equal.

x = a

And also, y° and b° are alternate interior angles and they are equal.

y = b

In (1), replace a by x and b by y.

x + y = 290

The correct answer choice is (D).

Question 4 :

In the figure above, lines a and b are parallel and QS bisects ∠PQR. What is the value of x?

A) 54

B) 60

C) 68

D) 72

Answer :

∠PQR and ∠QPT are alternate interior angles, hence they are equal.

∠PQR = ∠QPT

∠PQR = 108°

Since QS bisects ∠PQR,

∠SQR = (1/2)∠PQR

∠SQR = (1/2)(108°)

∠SQR = 54°

∠PSQ and ∠SQR are alternate interior angles, hence they are equal.

∠PSQ = ∠SQR

x° = 54°

The correct answer choice is (A).

Question 5 :

In the figure above, PQ || RS and QR || ST. What is the value of x?

A) 47

B) 51

C) 55

D) 57

Answer :

Since PQ || RS, ∠QPR and ∠SRT are corresponding angles, hence they are equal.

∠SRT = ∠QPR

∠SRT = x°

Since QR || ST, ∠QRP and ∠STR are corresponding angles, hence they are equal.

∠QRP = ∠STR

∠QRP = 65°

In the figure above,

∠QRP + ∠QRS + ∠SRT = 180°

∠QRP + ∠QRS + ∠SRT = 180°

65° + 68° + x° = 180°

133 + x = 180

x = 47

The correct answer choice is (A).

Question 6 :

In the figure above, p || q. What is the value of (a + b)?

A) 160

B) 175

C) 185

D) 200

Answer :

In the figure above, c° and 35° are vertical angles, hence they are equal.

c = 35

a + c = 90

Substitute c = 35.

a + 35 = 65

a = 30

Since p || q, b° and c° are consecutive interior angles, hence they are supplementary.

b + c = 180

b + 35 = 180

b = 145

a + b = 30 + 145

a + b = 175

The correct answer choice is (B).

Question 7 :

In the figure above, what is the value of (a + b)?

Answer :

In the given figure, draw ∠c as shown below.

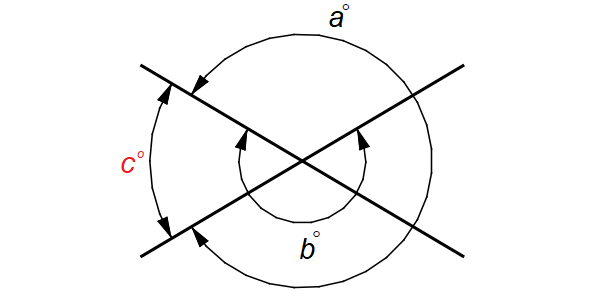
In the figure above,

a + c = 360 ----(1)

b - c = 180 ----(2)

(1) + (2) :

a + b = 540

Question 8 :

In the figure above, AB is parallel to DE. What is the measure of ∠BCD?

Answer :

In the given figure, draw CF, which is parallel to AB and DE as shown below.

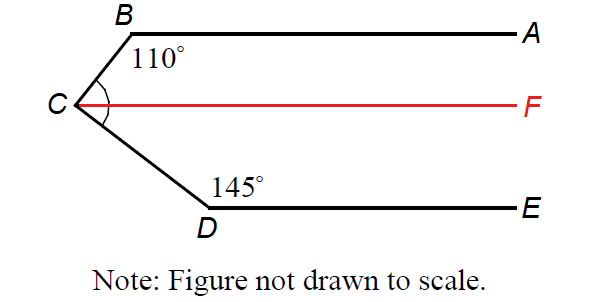
Since AB is parallel to CF, ∠ABC and ∠BCF are consecutive interior angles, hence they are supplementary.

∠ABC + ∠BCF = 180°

110° + ∠BCF = 180°

∠BCF = 70°

Since CF is parallel to DE, ∠FCD and ∠CDE are consecutive interior angles, hence they are supplementary.

∠FCD + ∠CDE = 180°

∠FCD + 145° = 180°

∠FCD = 35°

By the Angle Addition Postulate,

∠BCD = ∠BCF + ∠FCD

∠BCD = 70° + 35°

∠BCD = 105°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.