ANGLES IN A PARALLELOGRAM WORKSHEET

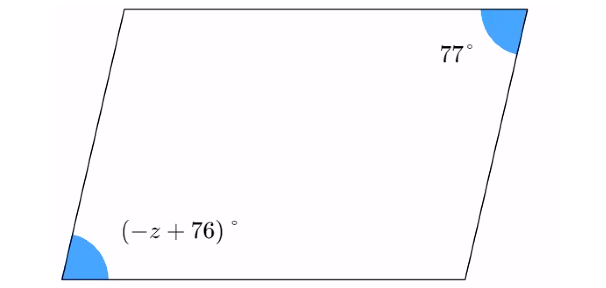
Problem 1 :

Solve for z in the parallelogram below.

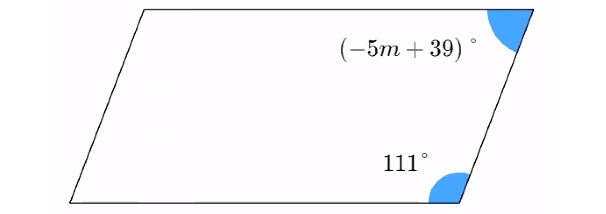
Problem 2 :

Solve for m in the parallelogram below.

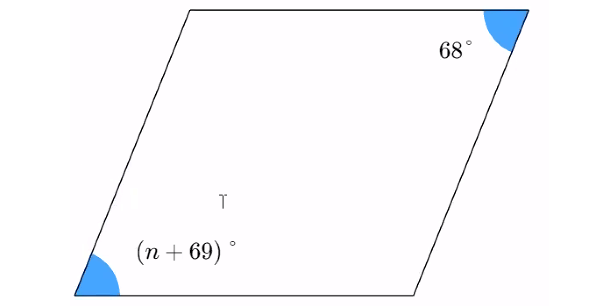
Problem 3 :

Solve for n in the parallelogram below.

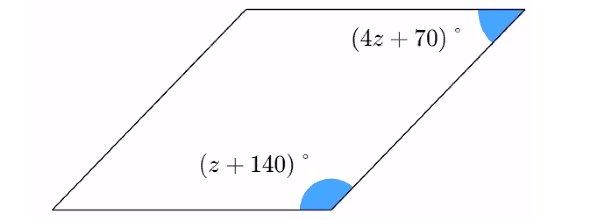
Problem 4 :

Solve for z in the parallelogram below.

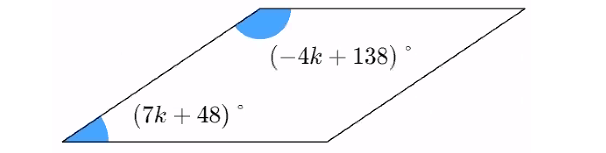
Problem 5 :

Solve for k in the parallelogram below.

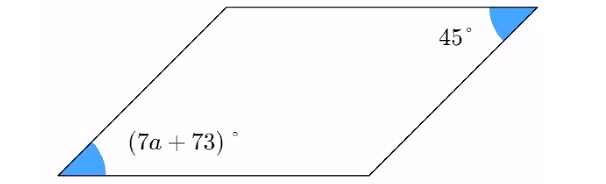
Problem 6 :

Solve for a in the parallelogram below.

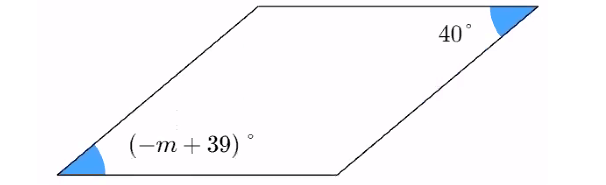
Problem 7 :

Solve for m in the parallelogram below.

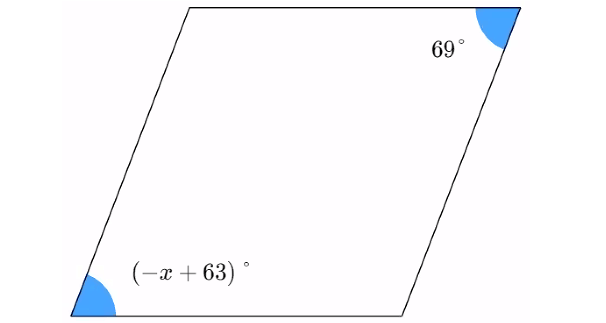
Problem 8 :

Solve for x in the parallelogram below.

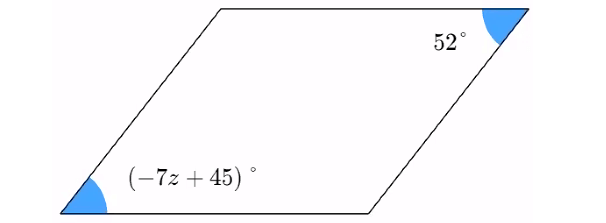
Problem 9 :

Solve for z in the parallelogram below.

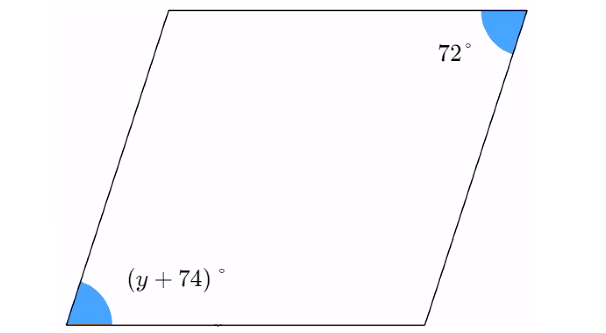
Problem 10 :

Solve for y in the parallelogram below.

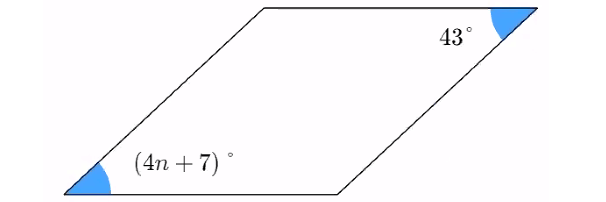
Problem 11 :

Solve for n in the parallelogram below.

Answers

1. Answer :

Opposite angles in a parallelogram are equal.

(-z + 76)° = 77°

-z + 76 = 77

Subtract 76 from both sides.

-z = 1

Multiply both sides by -1.

z = -1

2. Answer :

Adjacent angles in a parallelogram are supplementary.  That is, Adjacent angles in a parallelogram add up to 180°

(-5m + 39)° + 111° = 180°

-5m + 39 + 111 = 180

-5m + 140 = 180

Subtract 140 from both sides.

-5m = 40

Divide both sides by -5.

m = -8

3. Answer :

(n + 69)° = 68°

n + 69 = 68

Subtract 69 from both sides.

n = -1

4. Answer :

(z + 140)° + (4z + 70)° = 180°

z + 140 + 4z + 70 = 180

5z + 210 = 180

Subtract 210 from both sides.

5z = -30

Divide both sides by 5.

z = -6

5. Answer :

(7k + 48)° + (-4k + 138)° = 180°

7k + 48 + -4k + 138 = 180

3k + 186 = 180

Subtract 186 from both sides.

3k = -6

Divide both sides by 3.

z = -2

6. Answer :

(7a + 73)° = 45°

7a + 73 = 45

Subtract 73 from both sides.

7a = -28

Multiply both sides by 7.

a = -4

7. Answer :

(-m + 39)° = 40°

-m + 39 = 40

Subtract 39 from both sides.

-m = 1

Multiply both sides by -1.

m = -1

8. Answer :

(-x + 63)° = 69°

-x + 63 = 69

Subtract 63 from both sides.

-x = 6

Multiply both sides by -1.

x = -6

9. Answer :

(-7z + 45)° = 52°

-7z + 45 = 52

Subtract 45 from both sides.

-7z = 7

Divide both sides by -7.

z = -1

10. Answer :

(y + 74)° = 72°

y + 74 = 72

Subtract 74 from both sides.

y = -2

11. Answer :

(4n + 7)° = 43°

4n + 7 = 43

Subtract 7 from both sides.

4n = 36

Divide both sides by 4.

n = 9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.