ANGLES AND THEIR MEASUREMENT
About "Angles and their measurement"
Angles and their measurement :
An angle consists of two different rays that have the same initial point. The rays are the sides of the angles. The initial point is the vertex of the angle.
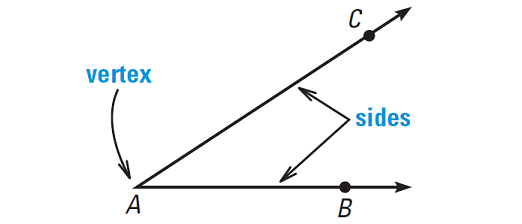
The angle that has sides AB and AC is denoted by ∠BAC, ∠CAB or ∠A. The point A is the vertex of the angle.
In this section, we are going to study two postulates about the measures of angles.
Postulate 1 (Protractor Postulate)
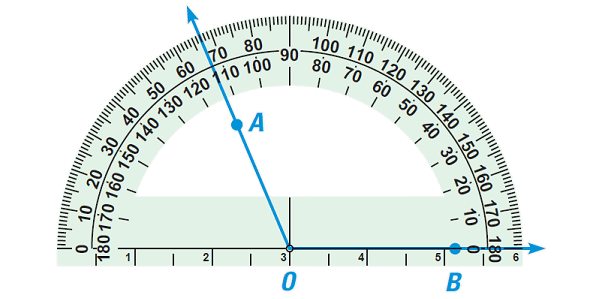
Consider a point A on one side of OB. The rays of the form OA can be matched one to one with the real numbers from 0 to 180.
The measure of ∠AOB is equal to the absolute value of the difference between the real numbers for OA and OB.
Postulate 2 (Angle Addition Postulate)
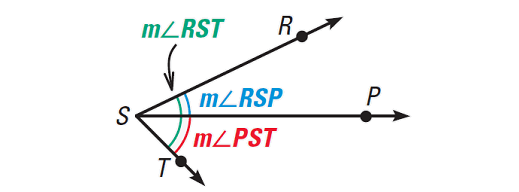
If P is in the interior of ∠RST, then we have
m∠RSP + m∠PST = m∠RST
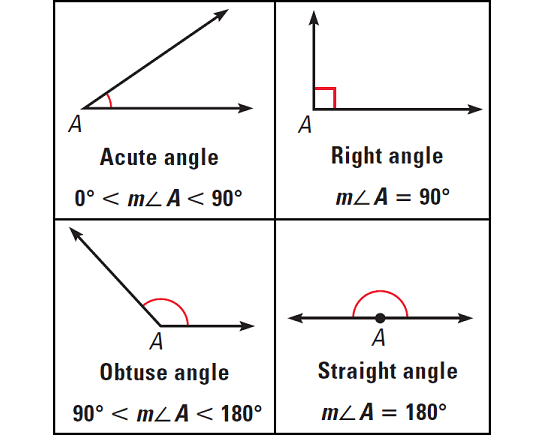
Classifying Angles
Angles are classified as acute, right, obtuse and straight, according to their measures. Angles have measures greater than 0°
Angles and their measurement - Examples
Example 1 :
Name the angles in the figure given below.
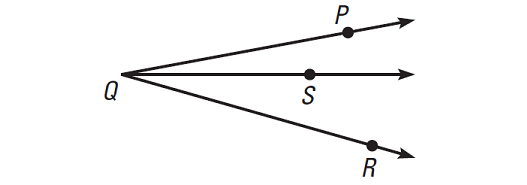
Solution :
There are three different angles.
∠PQS or ∠SQP
∠SQR or ∠RQS
∠PQR or ∠RQP
We should name any of the angles as ∠Q, because all three angles have Q as their vertex. The name ∠Q would not distinguish one angle from others.
Example 2 :
Each eye of a horse wearing blinkers has an angle of vision that measures 100°. The angle of vision that is seen by both eyes measures 60°.
Find the angle of vision seen by the left eye alone.
Solution :
We can use the angle addition postulate.
m∠2 + m∠3 = 100° (The total for left eye is 100°)
m∠3 = 100° - m∠2 (Subtract m∠2 from each side)
m∠3 = 100° - 60° (Substitute 60° for m∠2)
m∠3 = 40° (Subtract)
Hence, the vision for the left eye alone measures is 40°.
Example 3 :
Plot the points L (-4, 2), M(-1, -1), N (2, 2), Q(4, -1) and P(2, -4). Then, measure and classify the following angles as acute, right, obtuse or straight.
(i) m∠LMN
(ii) m∠LMP
(iii) m∠NMQ
(iv) m∠LMQ
Solution :
Plot the given points in xy coordinate plane.
We can use the protractor to measure and classify each angle as shown below.
|
MEASURE (i) m∠LMN = 90° (ii) m∠LMP = 180° (iii) m∠NMQ = 45° (iv) m∠LMQ = 135° |
CLASSIFICATION Right angle Straight angle Acute angle Obtuse angle |
Note :
Two angles are adjacent angles, if they share a common vertex and side, but have no common interior points.
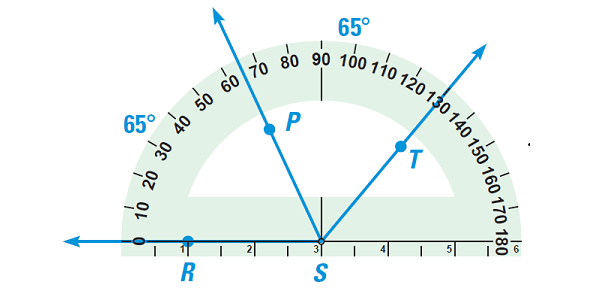
Example 4 :
Use a protractor to draw two adjacent acute angles ∠RSP and ∠PST so that ∠RST is
(a) Acute
(b) Obtuse
Solution :
Solution (a) :
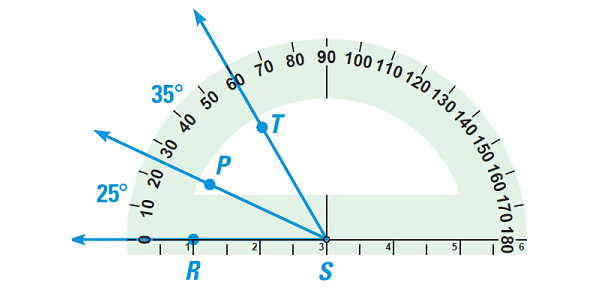
Solution (b) :
After having gone through the stuff given above, we hope that the students would have understood "Angles and their measurement".
Apart from the stuff given above, if you want to know more about "Angles and their measurement", please click here
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
