ANGLE THEOREMS FOR TRIANGLES WORKSHEET

Problem 1 : 

Can 30°, 60° and 90° be the angles of a triangle ?

Problem 2 : 

Can 35°, 55° and 95° be the angles of a triangle ?

Problem 3 : 

In a triangle, if the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle. 

Problem 4 : 

Find m∠W and m∠X in the triangle given below.

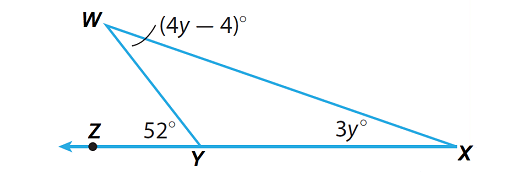
Problem 5 : 

Find m∠A and m∠B in the triangle given below.

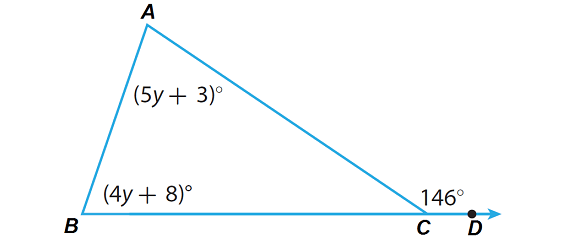
Detailed Answer Key

Problem 1 : 

Can 30°, 60° and 90° be the angles of a triangle ?

Solution :

Let us add all the three given angles and check whether the sum is equal to 180°.

 30° +  60° + 90°  =  180°

Since the sum of the angles is equal 180°, the given three angles can be the angles of a triangle. 

Problem 2 : 

Can 35°, 55° and 95° be the angles of a triangle ?

Solution :

Let us add all the three given angles and check whether the sum is equal to 180°.

 35° +  55° + 95°  =  185°

Since the sum of the angles is not equal 180°, the given three angles can not be the angles of a triangle. 

Problem 3 : 

In a triangle, if the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle. 

Solution :

Let x be the first angle.

The second angle  =  x + 5

The third angle  =  x + 5 + 5  =  x + 10

We know that,

the sum of the three angles of a triangle  =  180°

x + (x+5) + (x+10)  =  180°

3x + 15  =  180

3x  =  165

x  =  55

The first angle  =  55°

The second angle  =  55 + 5  =  60°

The third angle  =  60 + 5  =  65°

So, the three angles of a triangle are 55°, 60° and 65°. 

Problem 4 : 

Find m∠W and m∠X in the triangle given below.

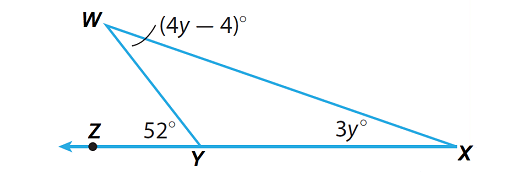
Solution : 

Step 1 : 

Write the Exterior Angle Theorem as it applies to this triangle.

m∠W + m∠X  =  m∠WYZ

Step 2 : 

Substitute the given angle measures.

(4y - 4)° + 3y°  =  52°

Step 3 : 

Solve the equation for y.

(4y - 4)° + 3y°  =  52°

4y - 4 + 3y  =  52

Combine the like terms. 

7y - 4  =  52

Add 4 to both sides.

7y - 4 + 4  =  52 + 4

Simplify.

7y  =  56

Divide both sides by 7. 

7y / 7  =  56 / 7

y  =  8

Step 4 : 

Use the value of y to find m∠W and m∠X.

So, m∠W  =  28° and m∠X  =  24°.

Problem 5 : 

Find m∠A and m∠B in the triangle given below.

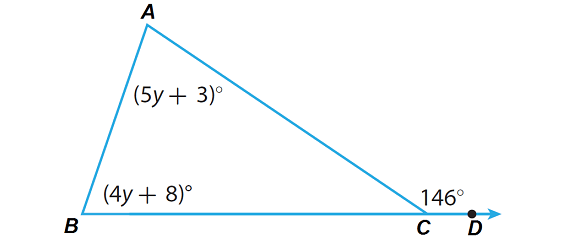
Solution : 

Step 1 : 

Write the Exterior Angle Theorem as it applies to this triangle.

m∠A + m∠B  =  m∠C

Step 2 : 

Substitute the given angle measures.

(5y + 3)° + (4y + 8)°  =  146°

Step 3 : 

Solve the equation for y.

(5y + 3)° + (4y + 8)°  =  146°

5y + 3 + 4y + 8  =  146

Combine the like terms. 

9y + 11  =  146

Subtract 11 from both sides.

9y + 11 - 11  =  146 - 11

Simplify.

9y  =  135

Divide both sides by 9. 

9y / 9  =  135 / 9

y  =  15

Step 4 : 

Use the value of y to find m∠A and m∠B.

So, m∠A  =  78° and m∠B  =  68°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.