ANGLE SUM PROPERTY OF TRIANGLE WORKSHEET

Question 1 :

Find the value of x.

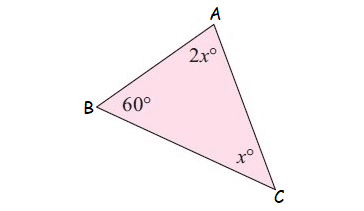
Question 2 :

Find the value of t.

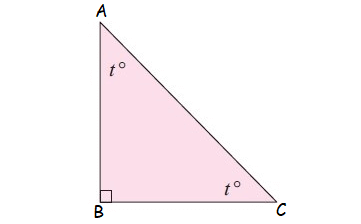
Question 3 :

Find the value of a.

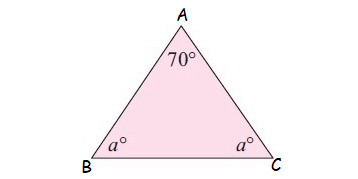
Question 4 :

Find the value of a.

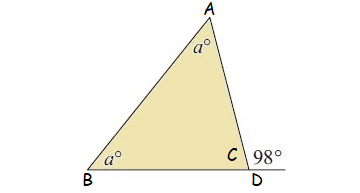
Question 5 :

Find the value of a.

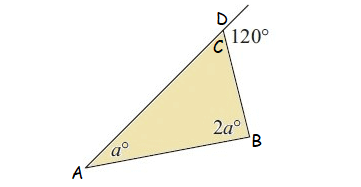
Question 6 :

Find the value of k.

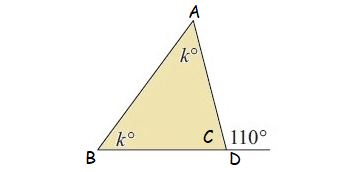
Question 7 :

Find the value of a.

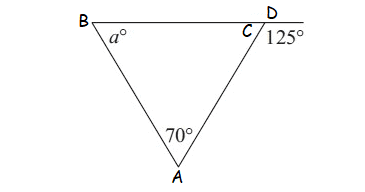
Question 8 :

Find the value of a.

Question 9 :

Find the value of a.

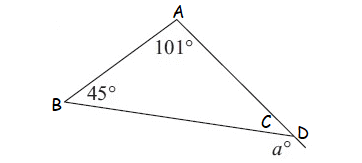
Question 10 :

Find the value of a.

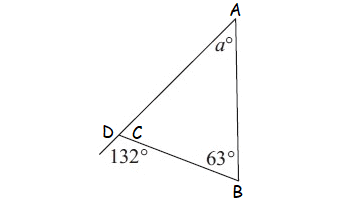
Question 11 :

Find the value of a.

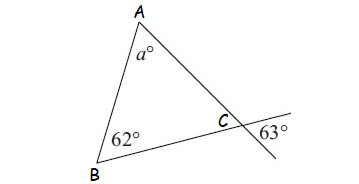
Question 12 :

Find the value of a.

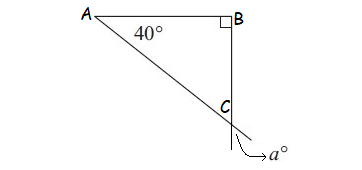
Answers

1. Answer :

In the triangle shown above, by Angle Sum Property of Triangle,

x° + 2x° + 60° = 180°

3x + 60 = 180

Subtract 60 from both sides.

3x = 120

Divide both sides by 3.

x = 40

2. Answer :

In the triangle shown above, by Angle Sum Property of Triangle,

t° + t° + 90° = 180°

2t + 90 = 180

Subtract 90 from both sides.

2t = 90

Divide both sides by 2.

t = 45

3. Answer :

In the triangle shown above, by Angle Sum Property of Triangle,

a° + a° + 70° = 180°

2a + 70 = 180

Subtract 70 from both sides.

2a = 110

Divide both sides by 2.

a = 55

4. Answer :

In the diagram shown above, C and 98° are linear pair.

C  + 98° = 180°

Subtract 98° from both sides.

C = 82°

In the triangle shown above, by Angle Sum Property of Triangle,

a° + a° + C = 180°

Substitute C = 82°.

a° + a° + 82° = 180°

2a + 82 = 180

Subtract 82 from both sides.

2a = 98

Divide both sides by 2.

a = 49

5. Answer :

In the diagram shown above, C and 120° are linear pair.

C  + 120° = 180°

Subtract 120° from both sides.

C = 60°

In the triangle shown above, by Angle Sum Property of Triangle,

a° + 2a° + C = 180°

Substitute C = 60°.

a° + 2a° + 60° = 180°

3a + 60 = 180

Subtract 60 from both sides.

3a = 120

Divide both sides by 3.

a = 40

6. Answer :

In the diagram shown above, C and 110° are linear pair.

C  + 110° = 180°

Subtract 110° from both sides.

C = 70°

In the triangle shown above, by Angle Sum Property of Triangle,

k° + k° + C = 180°

Substitute C = 70°.

k° + k° + 70° = 180°

2k + 70 = 180

Subtract 70 from both sides.

2k = 110

Divide both sides by 2.

k = 55

7. Answer :

In the diagram shown above, C and 125° are linear pair.

C  + 125° = 180°

Subtract 125° from both sides.

C = 55°

In the triangle shown above, by Angle Sum Property of Triangle,

a° + 70° + C = 180°

Substitute C = 55°.

a° + 70° + 55° = 180°

a + 125 = 180

Subtract 125 from both sides.

a = 55

8. Answer :

In the diagram shown above, a° and C are linear pair.

a° + C = 180°

Subtract a° from both sides.

C = 180° - a°

In the triangle shown above, by Angle Sum Property of Triangle,

C + 90° + 35° = 180°

Substitute C = 180° - a°.

180° - a° + 90° + 35° = 180°

-a + 305 = 180

Subtract 305 from both sides.

-a = -125

Multiply both sides by -1.

a = 125

9. Answer :

In the diagram shown above, a° and C are linear pair.

a° + C = 180°

Subtract a° from both sides.

C = 180° - a°

In the triangle shown above, by Angle Sum Property of Triangle,

C + 45° + 101° = 180°

Substitute C = 180° - a°.

180° - a° + 45° + 101° = 180°

-a + 326 = 180

Subtract 326 from both sides.

-a = -146

Multiply both sides by -1.

a = 146

10. Answer :

In the diagram shown above, C and 132° are linear pair.

C  + 132° = 180°

Subtract 132° from both sides.

C = 48°

In the triangle shown above, by Angle Sum Property of Triangle,

a° + 63° + C = 180°

Substitute C = 48°.

a° + 63° + 48° = 180°

a + 111 = 180

Subtract 111 from both sides.

a = 69

11. Answer :

In the diagram shown above, C and 63° are vertical angles.

C = 63°

In the triangle shown above, by Angle Sum Property of Triangle,

a° + 62° + C = 180°

Substitute C = 63°.

a° + 62° + 63° = 180°

a + 125 = 180

Subtract 125 from both sides.

a = 55

12. Answer :

In the diagram shown above, C and a° are vertical angles.

C = a°

In the triangle shown above, by Angle Sum Property of Triangle,

C + 40° + 90° = 180°

Substitute C = a°.

a° + 40° + 90° = 180°

a + 130 = 180

Subtract 130 from both sides.

a = 50

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.