ANGLE OF INCLINATION AND SLOPE OF A LINE

Let a straight line l intersect the x - axis at A. The angle between the positive x - axis and the line l, measured in counter  clockwise direction is called the angle of inclination of the straight line l. 

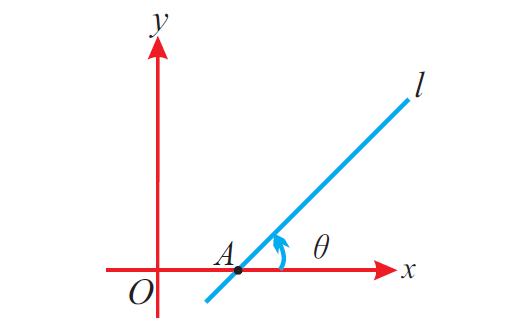
In the above figure, If θ is the angle of a straight line l, then we have the following important points.   

(i)  0° ≤ θ ≤ 180°

(ii)  For horizontal lines, θ  = 0° or 180° and for vertical lines, θ  =  90°

(iii)  If a straight line initially lies along the x-axis and starts rotating about a fixed point A on the x-axis in the counter clockwise direction and finally coincides with the x-axis, then the angle of inclination of the straight line in the initial position is 0°and that of the line in the final position is 0°. 

(iv)  Lines which are perpendicular to x-axis are called as vertical lines.

(v)  Lines which are perpendicular to y-axis are called as horizontal lines.

(vi)  Other lines which are neither perpendicular to x- axis and nor to y-axis are called as slant lines. 

Angle of Inclination and Slope of a Line - Application

The major application of angle of inclination of a straight line is finding slope. 

If θ is the angle of inclination of a straight line l, then tanθ is called the slope of gradient of the line is denoted by "m". 

Therefore, the slope of the straight line is 

m  =  tan θ 

for 0° ≤ θ ≤ 180°

Let us find the slope of a straight using the above formula 

(i)  For horizontal lines, the angle of inclination is 0° or 180°.

That is, 

θ  =  0° or 180°

Therefore, slope of the straight line is

m  =  tan0° or tan 180°  =  0

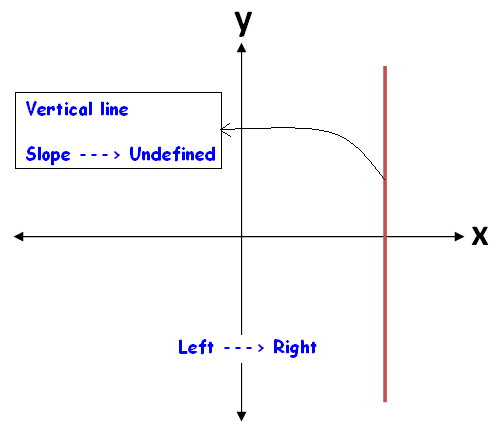
(ii) For vertical lines, the angle of inclination is 90°.

That is 

θ  =  90°

Therefore, slope of the straight line is

m  =  tan90°  =  Undefined

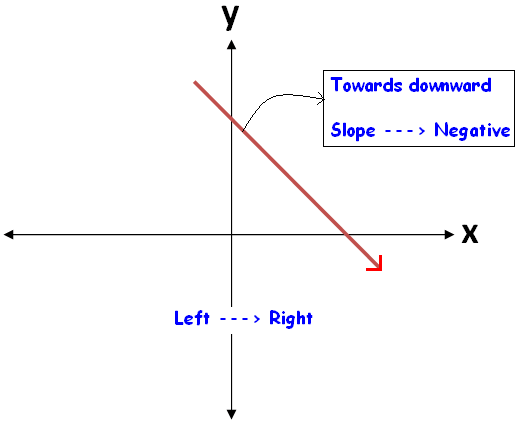
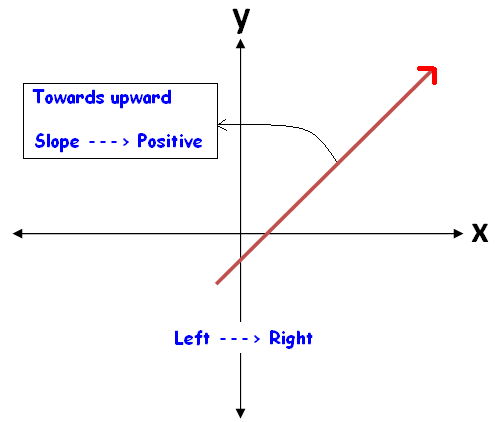
(iii) For slant lines, if θ is acute, then the slope is positive. Whereas if θ is obtuse, then the slope is negative.  

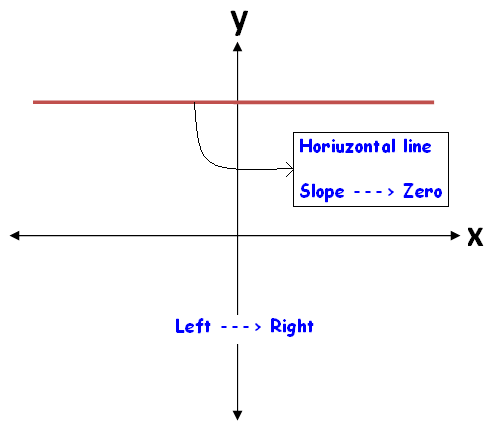
Slope of a line - Positive or Negative or Zero or Undefined

When we look at a straight line visually, we can come to know the sign of the slope easily.  

To know the sign of slope of a straight line, always we have to look at the straight line from left to right. 

The figures given below illustrate this. 

Solved Problems

Problem 1 :

Find the angle of inclination of the straight line whose slope is 1/√3.

Solution :

Let θ be the angle of inclination of the line. 

Then, slope of the line is

m  =  tanθ

Given : Slope = 1/√3

Then,  

1/√3  =  tanθ

θ  =  30°

So, the angle of inclination is 30°. 

Problem 2 :

If the angle of inclination of a straight line is 45°, find its slope. 

Solution :

Let θ be the angle of inclination of the line. 

Then, slope of the line,

m  =  tanθ

Given : θ  =  45°

Then,

m  =  tan 45°

m  =  1

So, the slope is 1. 

Problem 3 :

If the angle of inclination of a straight line is 30°, find its slope. 

Solution :

Let θ be the angle of inclination of the line. 

Then, slope of the line,

m  = tanθ

Given : θ  =  30°

Then, 

m  =  tan30°

m  =  1/√3

So, the slope is 1/√3. 

Problem 4 :

Find the angle of inclination of the straight line whose slope is √3.

Solution :

Let θ be the angle of inclination of the line. 

Then, slope of the line,  

m  = tanθ

Given : Slope  =  √3

Then, 

√3  =  tanθ  

θ  =  60°

So, the angle of inclination is 60°. 

Problem 5 :

Find the angle of inclination of the straight line whose equation is y = x + 32.

Solution :

Let θ be the angle of inclination of the line. 

The given equation is in slope intercept form.

That is,

y  =  mx + b

Comparing

y  =  x + 32

and

y  =  mx + b,

we get the slope m  =  1. 

We know that the slope of the line is

m  =  tanθ

Then,

1  =  tanθ

θ  =  45°

So, the angle of inclination is 45°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.