ANGLE OF ELEVATION AND DEPRESSION WORKSHEET

1. The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30° . If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiations control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms.

2. The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find (i) The height of the lamp post. (ii) The difference between height of the lamp post and the apartment. (iii) The distance between the lamp post and the apartment. (√3 = 1.732)

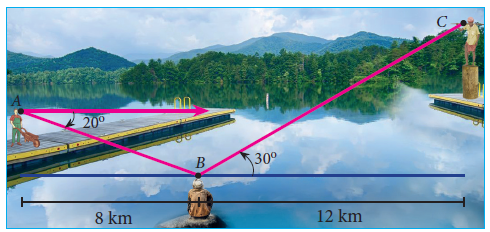
3. Three villagers A, B and C can see each other across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30° . Calculate : (i) the vertical height between A and B. (ii) the vertical height between B and C. (tan 20° = 0.3640, √3 = 1.732)]

4. Two men on either side of a temple of 30 meter height observe its top at the angles of elevation 30º and 60º respectively. Find the distance between the two men.

5. A straight highway leads to the foot of a tower. Ramaiah standing at the top of the tower observes a car at an angle of depression 30º. The car is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60º. Find the time taken by the car to reach the foot of the tower from this point.

6. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

1. Answer :

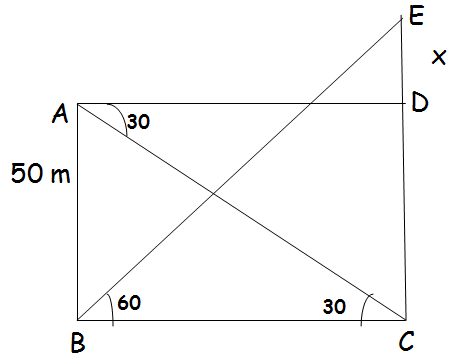
In triangle BEC,

tanθ = Opposite side/Adjacent side 

tan60° = EC/BC

√3 = (50 + x)/BC

BC = (50 + x)/√3 ----(1)

In triangle ABD,

tan30° = AB/BC

1/√3 = 50/BC

BC = 50√3 ----(2)

(1) = (2)

(50 + x)/√3 = 50√3

50 + x = 50√3√3

50 + x = 150

x = 150 - 50

x = 100

Height of cell phone tower = 100 + 50

  = 150 m

Hence the cell phone tower meets the radiation norms.

2. Answer :

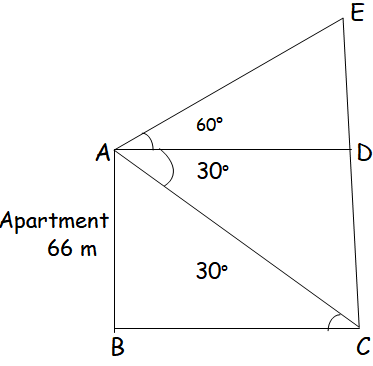
In triangle AED,

tan 60 = ED/AD

√3 = ED/AD

AD = ED/√3 ----(1)  

In triangle ABC,

tan 30 = AB/BC

1/√3 = 66/BC

BC = 66√3 ----(2)  

(1) = (2)

ED/√3 = 66√3

ED = 66(3)

ED = 198

(i)  Height of lamp post = ED + DC

= 198 + 66

= 264 m

(ii) The difference between height of the lamp post and the apartment

= 264 - 66

= 198 m

(iii) The distance between the lamp post and the apartment

BC = 66√3

= 66(1.732)

= 114.31 m

3. Answer : 

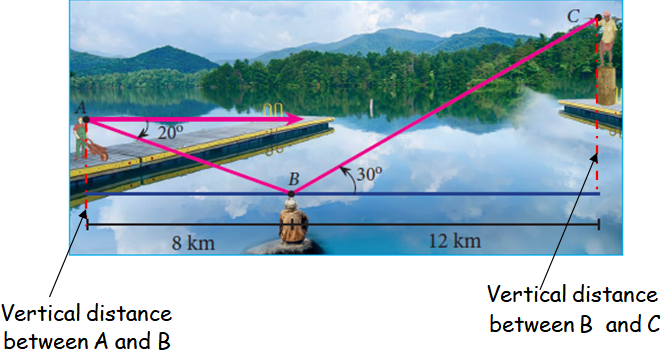
In the left side triangle,

tan 20 = Vertical distance of AB/8

 0.3640 = Vertical distance of AB/8

Vertical distance of AB = 0.3640(8)

Vertical distance of AB = 2.91 km

In the right side triangle,

tan 30 = Vertical distance of BC/12

1/√3 = Vertical distance of BC/12

Vertical distance of BC = 12/√3

= 12(√3/3)

= 4√3

= 4(1.732)

= 6.928

Vertical distance of BC = 6.93 km.

4. Answer : 

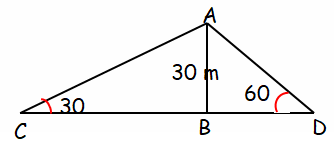
In triangle ABC, 

tan 30 = Opposite side / Adjacent side

1/√3 = AB/BC

1/√3 = 30/BC

BC = 30√3 --------(1)

In triangle ABD,

tan 60 = AB/BD

√3 = 30/BD

BD = 30/√3 --------(2)

CD = BC + BD

= 30√3 + (30/√3)

Rationalizing the denominator, we get

= 30√3 + 10√3

= 40√3

Applying the value of √3 as 1.732, we get

= 40(1.732)

= 69.28 m

So, the distance between two men is 69.28 m.

5. Answer : 

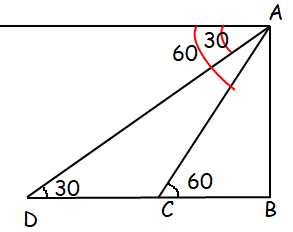
In triangle ADB,

Time = distance / speed

Let x be the speed of car. Time taken to reach C is 6 seconds.

Distance between DC = 6x

tan 30 = AB/DB

1/√3 = AB/(DC + BC)

1/√3 = AB/(6x + BC)

(6x + BC) / √3 = AB 

AB = (6x + BC) / √3 ----------(1)

In triangle ABC,

tan 60 = AB/BC

√3 = AB/BC

AB = √3 BC --------(2)

(1) = (2)

(6x + BC) / √3 = √3 BC

6x + BC = 3BC

6x = 3BC - BC

2BC = 6x

BC = 6x/2

BC = 3x

x represents the uniform speed, the time taken to reach the tower is 3 seconds.

6. Answer :

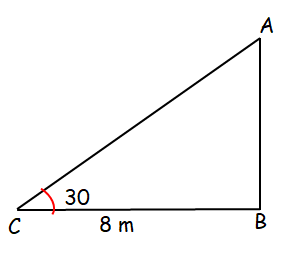
tan 30 = AB/BC

1/√3 = AB/8

AB = 8/√3

Applying the value of √3 as 1.732, we get

AB = 4.61 m

So, the height of the tree is 4.61 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.