ANGLE MEASURES IN TRIANGLES WORKSHEET

1. The measure of one acute angle of a right triangle is two times the measure of the other acute angle. Find the measure of each acute angle. 

2. Find the missing angles in the triangle shown below. 

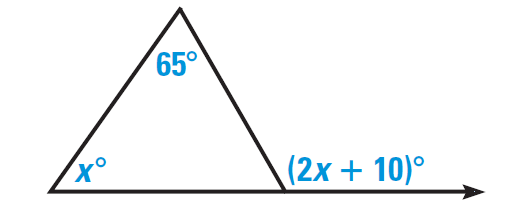
3. Find the value of x in the diagram shown below. 

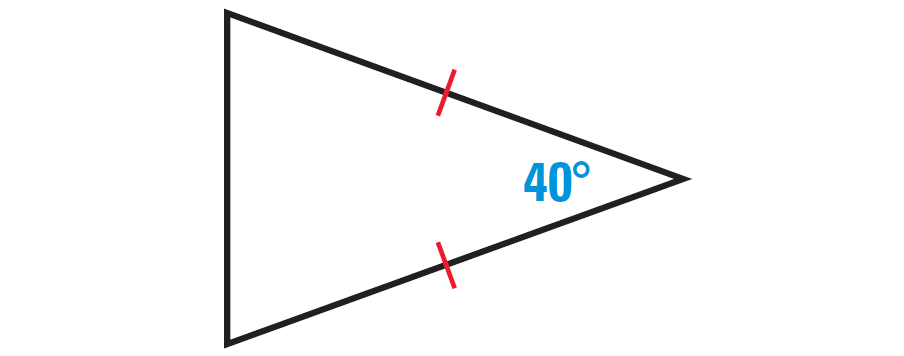
4. Find the missing angles in the triangle shown below. 

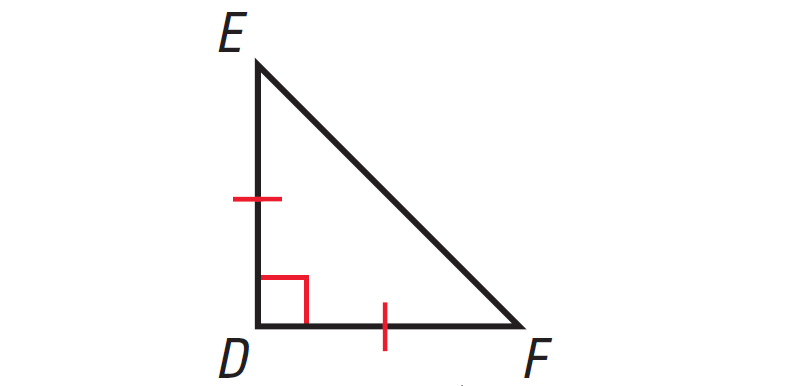
5.

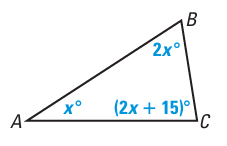
6.

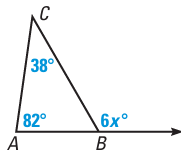
7.

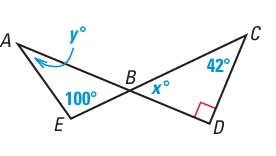
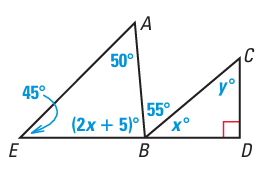
8.

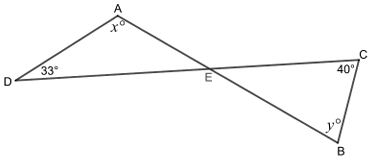
9. In the figure below, AB intersects CD atE. If x = 106, what is the value of y ?

(A) 41     (B) 74    (C) 99    (D) 106

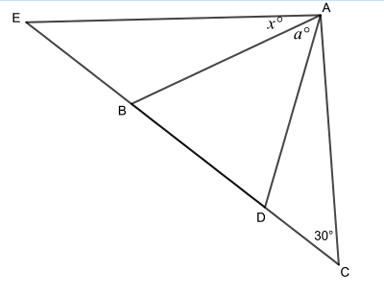
10. In the figure below, AC = AE and AB = AD and the value of a is 20. What is the value of x ?

1. Answer :

Let A, B and C be the vertices of the triangle and right angle is at C. 

Let ∠A = x°, then ∠B = 2x°. The diagram shown below illustrates this. 

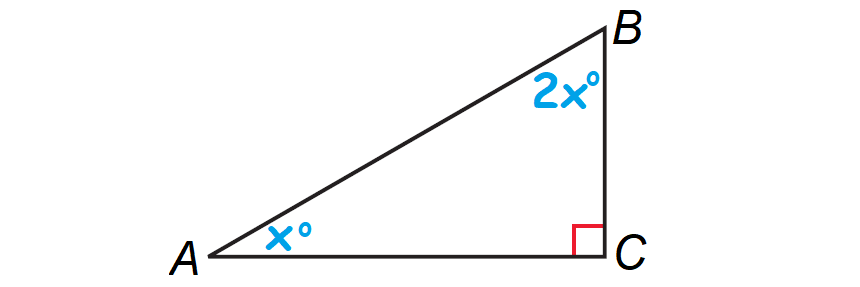
By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.  

x° + 2x° = 90°

3x° = 90°

Divide both sides by 3.

x = 30

So, m∠A = 30° and m∠B = 2(30°) = 60°.

Hence, the two acute angles are 30° and 60°. 

2. Answer :

In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent. 

So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent. 

The diagram shown below illustrates this. 

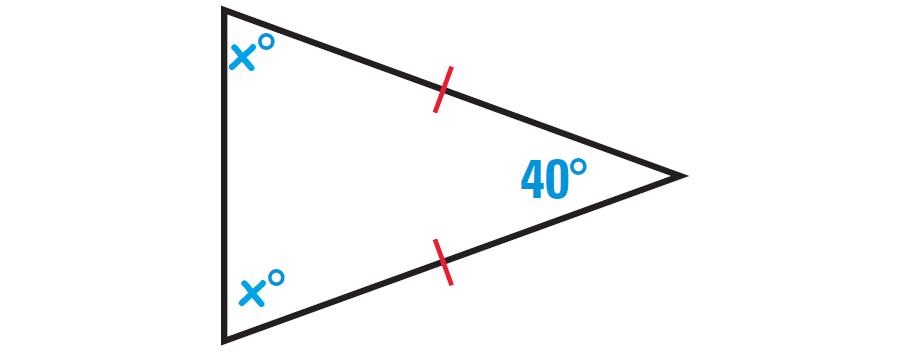
By Triangle Sum Theorem, the sum of the measures of the interior angles of a triangle is 180°. 

x° + x° + 40° = 180°

2x + 40 = 180

Subtract 40 from both sides. 

2x = 140

Divide both sides by 2. 

x = 70 

Hence, the measure of each missing angle is 70°.

3. Answer :

By Exterior Angle Theorem, the measure of an exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles. 

x° + 65° = (2x + 10)°

x + 65 = 2x + 10

Subtract x from both sides. 

65 = x + 10

Subtract 10 from both sides. 

55 = x

4. Answer :

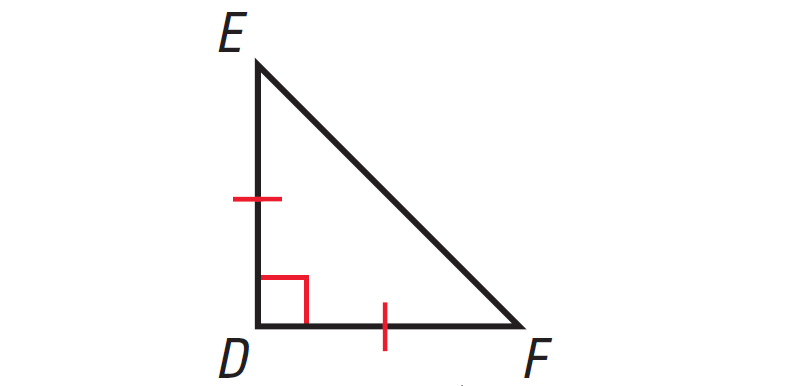
In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent. 

So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent. 

The diagram shown below illustrates this. 

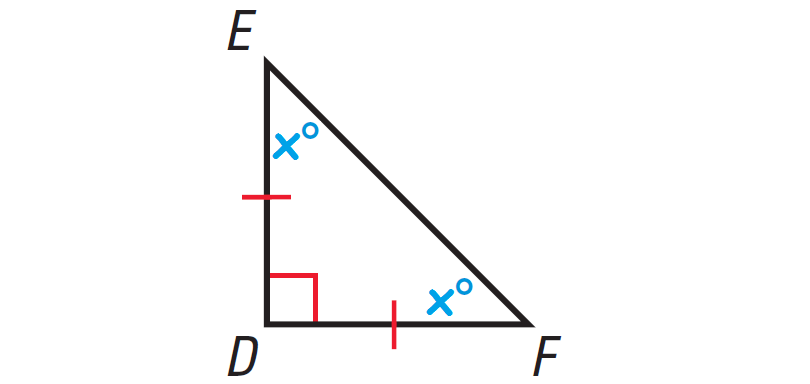
In the triangle shown above, one of the angles is right angle. So, it is right triangle.

By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.  

x° + x° = 90°

2x = 90

Divide both sides by 2. 

x = 45

Hence, the measure of each missing angle is 45°.

5. Answer :

Sum of interior angles of triangle = 180

x + 2x + 15 + 2x = 180

5x + 15 = 180

5x = 180 - 15

5x = 165

x = 165/5

x = 33

So, the value of x is 33.

6. Answer :

Exterior angle = Sum of remote interior angles

6x = 38 + 82

6x = 120

x = 120/6

x = 20

So, the value of x is 20.

7. Answer :

In triangle BCD,

x + 90 + 42 = 180

x + 132 = 180

x = 180 - 132

x = 48

Vertical opposite angles will be equal, then <ABE = 48

In triangle AEB,

y + 48 + 100 = 180

y + 148 = 180

y = 180 - 148

y = 32

8. Answer :

In triangle AEB,

45 + 50 + 2x + 5 = 180

2x + 100 = 180

2x = 180 - 100

2x = 80

x = 80/2

x = 40

In triangle BCD,

x + y + 90 = 180

x + y = 180 - 90

x + y = 90

Applying the value of x, we get

40 + y = 90

y = 90 - 40

y = 50

9. Answer :

In the triangle AED,

x + 33 + <AED = 180

Given that x = 106

106 + 33 + <AED = 180

139 + <AED = 180

<AED = 180 - 139

<AED = 41

Vertical angles are equal.

<CEB = 41

In triangle CEB,

<CEB + 40 + y = 180

41 + 40 + y = 180

81 + y = 180

y = 180 - 81

y = 99

So, the value of y is 99.

10. Answer :

Since AC = AE

<ACE = <AEC = 30

Since AB = AD

<ABD = <ADB

In triangle ABD,

<BAD + <ABD + <ADB = 180

a + <ABD + <ABD = 180

20 + 2<ABD = 180

2<ABD = 180 - 20

2<ABD = 160

<ABD = 160/2

<ABD = 80

Using exterior angle theorem,

<BEA + <BAE = <ABD

<BEA + x = 80

30 + x = 80

x = 80 - 30

x = 50

So, the value of x is 50.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.