ANGLE MEASURES IN POLYGONS WORKSHEET

Problem 1 :

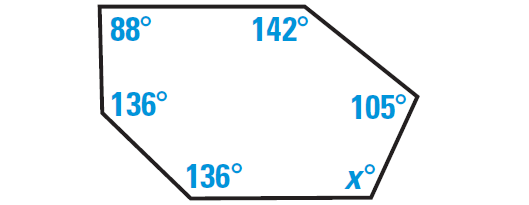
Find the value of x in the diagram shown below.

Problem 2 :

The measure of each interior angle of a regular polygon is 140°. How many sides does the polygon have ?

Problem 3 :

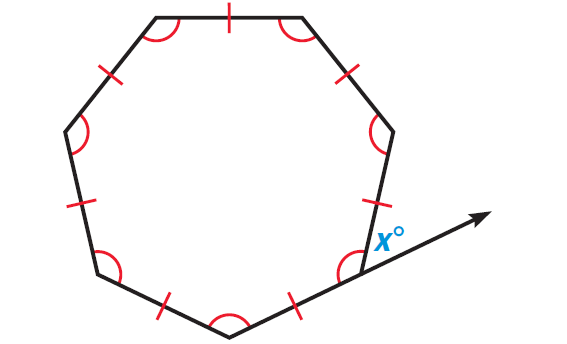
Find the value of x in the regular polygon shown below.

Problem 4 :

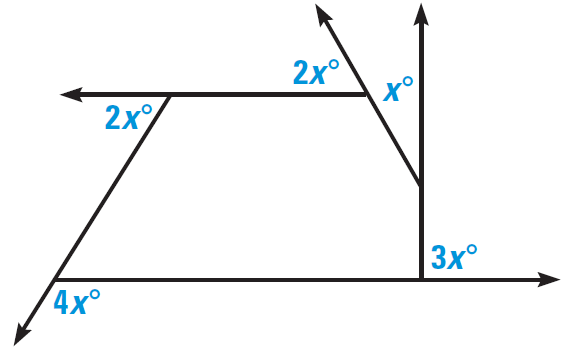
Find the value of x in the diagram shown below.

Problem 5 :

A home plate maker for a soft ball field is a pentagon. Three of the interior angles of the pentagon are right angles. The remaining two interior angles are congruent. What is the measure of each angle ?

Problem 6 :

If we were designing the home plate marker for some new type of ball game, would it be possible to make a home plate marker that is a regular polygon with each interior angle having a measure of (a) 135° ? (b) 145° ?

Answers

1. Answer :

The polygon shown in the diagram above has 6 sides. So it is hexagon. 

The sum of the measures of the interior angles of any hexagon is

=  (6 - 2) ⋅ 180°

=  4 ⋅ 180°

=  720°

We can add the measures of all interior angles of the above hexagon and the sum can be equated to 720°.

So, we have

136° + 136° + 88° + 142° + 105° + x°  =  720°

Simplify.

607 + x  =  720

Subtract 607 from each side. 

x  =  113

Hence, the measure of sixth interior angle of the hexagon is 113°.

2. Answer :

By Polygon Interior Angles Theorem, we have

[(n - 2) ⋅ 180°]/n  =  140°

Multiply each side by n. 

(n - 2) ⋅ 180  =  140n

Simplify.

180n - 360  =  140n

Subtract 140n from each side. 

40n - 360  =  0

Add 360 to each side. 

40n  =  360

Divide each side by 40. 

40n/40  =  360/40

n  =  9

Hence, the polygon has 9 sides and it is a regular nonagon.

3. Answer :

The polygon shown above is regular and it has 7 sides. So, it is a regular heptagon and the measure of each exterior angle is x°. 

By the Polygon Exterior Angles Theorem, we have

x°  =  1/7 ⋅ 360°

Simplify.

x  ≈  51.4

Hence, the measure of each exterior angle of a regular heptagon is about 51.4°.

4. Answer :

The polygon shown in the diagram above has 5 sides. So it is pentagon. 

The sum of the measures of the exterior angles of a convex polygon, one angle at each vertex is

=  360°

We can add the measures of all exterior angles of the above pentagon and the sum can be equated to 360°.

So, we have

2x° + x° + 3x° + 4x° + 2x°  =  360°

Simplify.

12x  =  360

Divide each side by 12.

12x/12  =  360/12

x  =  30

5. Answer :

Draw a Sketch : 

Sketch and label a diagram for the above plate maker. It is a non regular pentagon.

Let ∠A, ∠B and ∠D be the right angles.

Let ∠C and ∠E be the remaining two congruent angles. 

So, we have 

∠C  ≅  ∠E

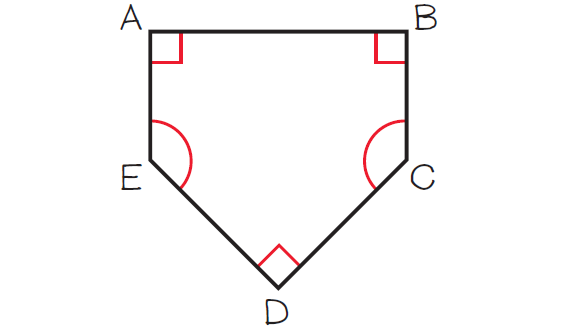
The sum of the measures of the interior angles of a pentagon is 

=  (5 - 2) ⋅ 180°

=  3 ⋅ 180°

=  540°

Verbal Model :

Labels :

Sum of measures of interior angles  =  540°

Measure of each right angle  =  90°

Measure of ∠C and ∠E  =  x°

Reasoning : 

Write the equation.

540°  =  3 ⋅ 90° + 2x°

Simplify.

540  =  270 + 2x

Subtract 270 from each side. 

270  =  2x

Divide each side by 2. 

270/2  =  2x/2

135  =  x

Hence, the measure of each of the two congruent angles is 135°.

6. Answer :

Solution (a) :

Let n be the number of sides of the regular polygon.

By Polygon Interior Angles Theorem, we have

[(n - 2) ⋅ 180°] / n  =  135°

Multiply each side by n. 

(n - 2) ⋅ 180  =  135n

180n - 360  =  135n

Subtract 135n from each side. 

45n - 360  =  0

Add 360 to each side. 

45n  =  360

Divide each side by 45.

45n/45  =  360/45

n  =  8

Yes, it would be possible. Because a polygon can have 8 sides. 

Solution (b) :

Let n be the number of sides of the regular polygon.

By Polygon Interior Angles Theorem, we have

[(n - 2) ⋅ 180°] / n  =  145°

Multiply each side by n. 

(n - 2) ⋅ 180  =  145n

180n - 360  =  145n

Subtract 145n from each side. 

35n - 360  =  0

Add 360 to each side. 

35n  =  360

Divide each side by 35.

35n/35  =  360/35

n  ≈  10.3

No, it would not be possible. Because, a polygon can not have 10.3 sides. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.