ANGLE BETWEEN TWO VECTORS USING CROSS PRODUCT

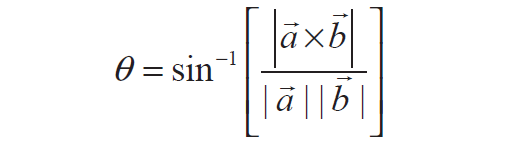
Example 1 :

Find the angle between the following two vectors using cross product.

2i + j - k 

i + 2j + k

Solution :

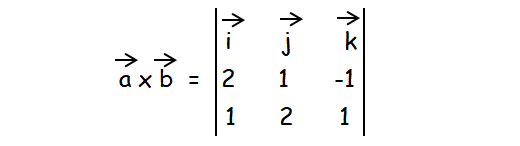
  |a x b| =  i[1 + 2] - j[2 + 1] + k[4 - 1]

  |a x b| =  3i - 3j + 3k

|a x b|² = √(3² + (-3)² + 3²) = 3√3

|a| = √(2² + 1² + (-1)²) = √6

|b| = √(1² + 2² + 1²) = √6

θ = sin^-1(3√3/√6√6)

θ = sin^-1(3√3/6)

= sin^-1(√3/2)

= π/3

Example 2 :

Let a vector, b vector, c vector be unit vectors such that a ⋅ b = a ⋅ c = 0 and the angle between b vector and c vector is π/3. Prove that a vector = ±(2/√3)(b x c).

Solution :

From given information, we have a ⋅ b = a ⋅ c = 0.

From this we may decide that a vector is perpendicular to b vector and a vector is perpendicular to c vector.

a vector is perpendicular to both b vector and c vector. So, a vector is proportional to (b x c) vector

a vector = ± λ(b x c)

|a| = ±λ|(b x c| ----(1)

|a| = ±λ|b||c|sinθ

1 = ±λsin(π/3)

λ = 2/√3

Substituting λ = 2/√3 in (1), 

a vector = ±(2/√3)(b x c)

Example 3 :

For any vector a vector prove that

|a x i|² + |a x j|²+ |a x k|² = 2|a|²

Solution :

Let a vector = xi + yj + zk. 

a x i : 

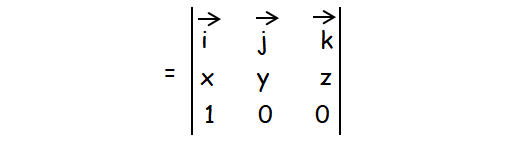
= i[0 - 0] - j[0 - z] + k[0 - y]

a x i = zj - yk

|a x i| = √(z² + (-y)²) = √(z² + y²)

|a x i|² = z² + y² ----(1)

a x j : 

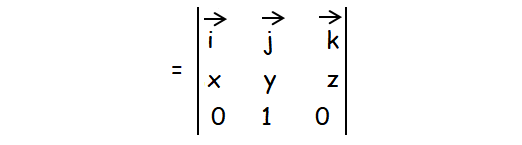
= i[0 - z] - j[0 - 0] + k[x - 0]

a x j = -zi + xk

|a x j| = √((-z)² + x²) = √(z² + x²)

|a x j|² = z² + x² ----(2)

Similarly,  

a x k = i[y - 0] - j[x - 0] + k[0 - 0]

a x k = yi - xj

|a x k| = √(y² + (-x)²) = √(y² + x²)

|a x k|² = y² + x² ----(3)

(1) + (2) + (3) :  

|a x i|² +|a x j|² + |a x k|² = (z² + y²) + (z² + x²) + (y² + x²)

= z² + y² + z² + x² + y² + x²

= 2x² + 2y² + 2z²

= 2(x² + y² + z)²

= 2|a|²

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.