ANGLE ANGLE SIMILARITY

Similar figures have the same shape but may have different sizes. Two triangles are similar if their corresponding angles are congruent and the lengths of their corresponding sides are proportional.

Angle-Angle (AA) Similarity Postulate

If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

Discovering Angle Angle Similarity

Step 1 :

Use your protractor and a straightedge to draw a triangle. Make one angle measure 45° and another angle measure 60°.

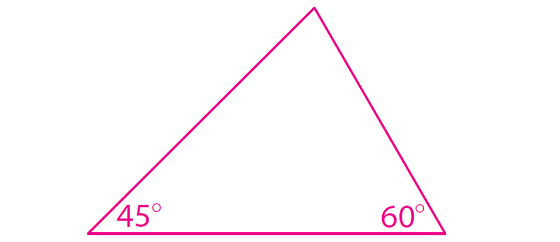
Step 2 : 

Compare your triangle to those drawn by your classmates. Triangle drawn by you and the triangles drawn by your classmates will have same shape and different in sizes.

Step 3 : 

Use the Triangle Sum Theorem to find the measure of the third angle of your triangle.

180° - (45° + 60°)  =  180° - 105°  =  75°

Reflect

1. If two angles in one triangle are congruent to two angles in another triangle, what do you know about the third pair of angles ?

They must also be congruent.

2.  Are two pairs of congruent angles enough information to conclude that two triangles are similar ? Explain.

Yes

By the Triangle Sum Theorem, the third pair of angles must have the same angle measure and thus are congruent, so the triangles must be similar.

Solved Problems

Problem 1 :

Explain whether the triangles PQR and STU  are similar.

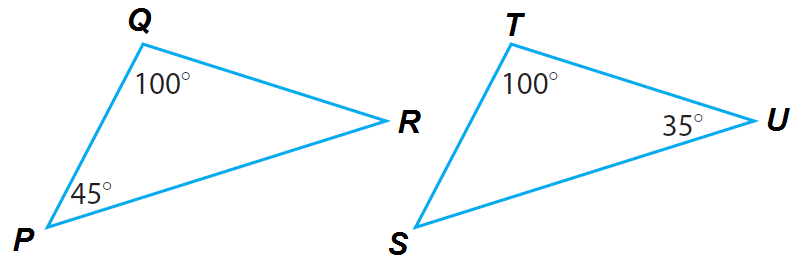
Solution :

The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle PQR : 

Write the Triangle Sum Theorem for this triangle.

m∠P + m∠Q + m∠R  =  180°

Substitute the given angle measures.

45° + 100° + m∠R  =  180°

Simplify.

145° + m∠R  =  180°

Subtract 145° from both sides.

145° + m∠R - 145°  =  180° - 145°

Simplify.

m∠R  =  35°

Triangle STU : 

Write the Triangle Sum Theorem for this triangle.

m∠S + m∠T + m∠U  =  180°

Substitute the given angle measures.

m∠S + 100° + 35°  =  180°

Simplify.

m∠S + 135°  =  180°

Subtract 135° from both sides.

m∠S + 135° - 135°  =  180° - 135°

Simplify.

m∠S  =  45°

Conclusion :

Three Angles of triangle PQR are 45°, 100° and 35°.

Three Angles of triangle STU are 45°, 100° and 35°.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Problem 2 :

Explain whether the triangles ABC and DEF  are similar.

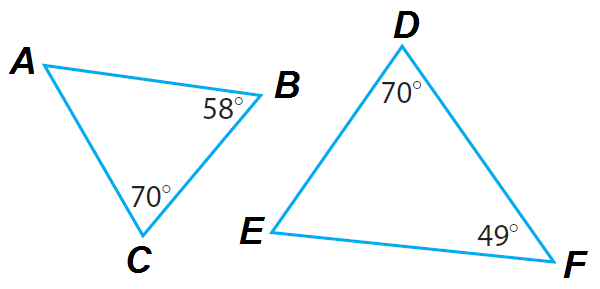
Solution :

The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle ABC : 

Write the Triangle Sum Theorem for this triangle.

m∠A + m∠B + m∠C  =  180°

Substitute the given angle measures.

m∠A + 58° + 70°  =  180°

Simplify.

m∠A + 128°  =  180°

Subtract 128° from both sides.

m∠A + 128° - 128°  =  180° - 128°

Simplify.

m∠A  =  52°

Triangle DEF : 

Write the Triangle Sum Theorem for this triangle.

m∠D + m∠E + m∠F  =  180°

Substitute the given angle measures.

70° + m∠E + 49°  =  180°

Simplify.

m∠E + 119°  =  180°

Subtract 119° from both sides.

m∠E + 119° - 119°  =  180° - 119°

Simplify.

m∠E  =  61°

Conclusion :

Three Angles of triangle ABC are 52°, 58° and 70°.

Three Angles of triangle DEF are 70°, 61° and 49°.

Because only one angle is congruent, the two triangles are not similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.