ANALYZING GRAPH WORKSHEET

Question 1 :

Ken has a weekly goal of burning 2400 calories by taking brisk walks. The equation y = -300x + 2400 represents the number of calories y Ken has left to burn after x hours of walking which burns 300 calories per hour.After how many hours of walking will Ken have 600 calories left to burn ? After how many hours will he reach his weekly goal ?

Question 2 :

Jose wants to buy a new game system that costs $200. He does not have enough money to buy it today, so he compares layaway plans at different stores. Store A requires an initial payment of $60 and weekly payments of $20 until the balance is paid in full. The plan at Store B is shown on the graph.

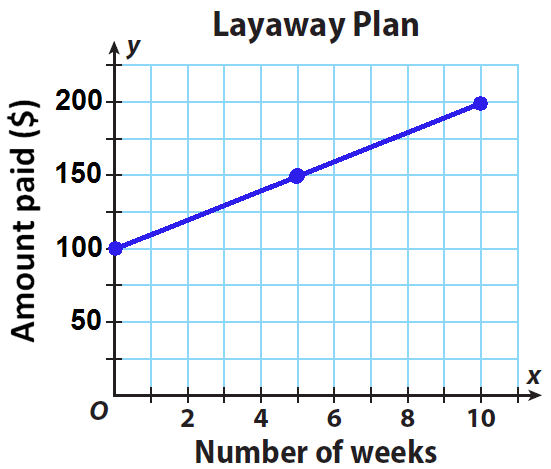
Based on the information given above, find which store allows Jose to pay for the game system faster. 

Question 3 : 

A roller coaster park is open from May to October each year. The graph shows the number of park visitors over its season.

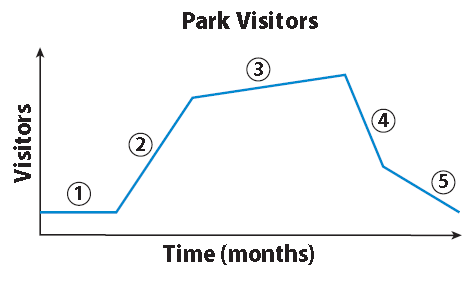
Answer the following Questions

(i) Segment 1 shows that attendance during the opening weeks of the park’s season stayed constant. Describe what Segment 2 shows.

(ii) Based on the time frame, give a possible explanation for the change in attendance represented by Segment 2.

(iii) Which segments of the graph show decreasing attendance? Give a possible explanation.

(iv) Explain how the slope of each segment of the graph is related to whether attendance increases or decreases.

Detailed Answer Key

Question 1 :

Ken has a weekly goal of burning 2400 calories by taking brisk walks. The equation y = -300x + 2400 represents the number of calories y Ken has left to burn after x hours of walking which burns 300 calories per hour.After how many hours of walking will Ken have 600 calories left to burn ? After how many hours will he reach his weekly goal ?

Answer : 

Step 1 :

 y = -300x + 2400

The y-intercept is b = 2400. Plot the point that contains the y-intercept : (0, 2400).

Step 2 : 

Write the slope as a fraction.

m  =  -300/1  =  -600/2  =  -900/3

Using the slope as -900/3 helps in drawing a more accurate graph.

The slope is m = -900/3. Use the slope to find second a point. Since the slope  =  rise / run, from (0, 2400), count down 900 units and right 3 units. 

Then, the new point is (3, 1500). 

Step 3 : 

Draw a line through the points. 

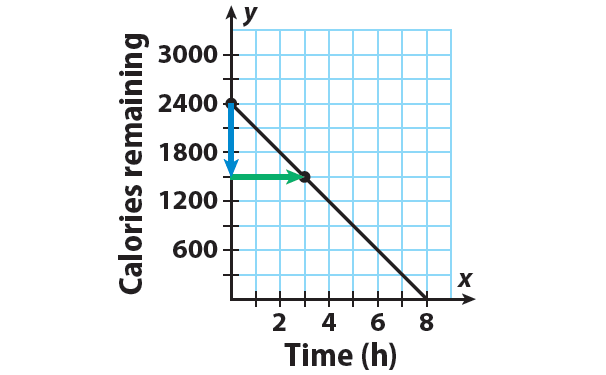
Step 4 : 

To find after how many hours of walking will Ken have 600 calories left to burn, 

Locate 600 calories on the y-axis. Read across and down to the x-axis.

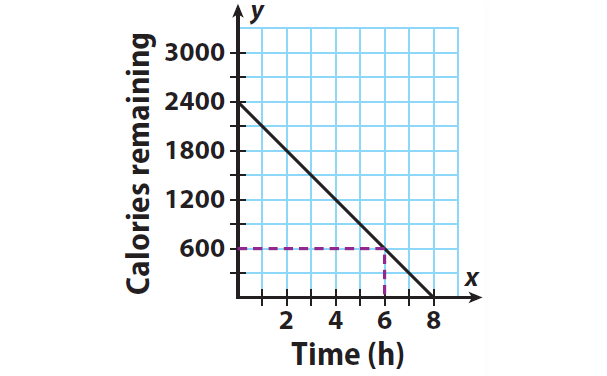
From the graph, we can know that Ken will have 600 calories left to burn after 6 hours.

Step 5 : 

Ken will reach his weekly goal when the number of calories left to burn is 0. Because every point on the x-axis has a y-value of 0, find the point where the line crosses the x-axis.

Ken will reach his goal after 8 hours of brisk walking.

Question 2 :

Jose wants to buy a new game system that costs $200. He does not have enough money to buy it today, so he compares layaway plans at different stores. Store A requires an initial payment of $60 and weekly payments of $20 until the balance is paid in full. The plan at Store B is shown on the graph.

Based on the information given above, find which store allows Jose to pay for the game system faster. 

Answer : 

Step 1 :

To find which store allows Jose to pay for the game system faster, let us have the deals offered by store A and B as equations.

Write an equation in slope-intercept form for Store A’s layaway plan.

Let x represent number of weeks and y represent the total money to be paid.

y  =  20x + 60

Step 2 :

Write an equation in slope-intercept form for Store B’s layaway plan.

Let x represent number of weeks and y represent the total money to be paid. 

From the graph, y - intercept is 100 and the slope is 10

y  =  10x + 100

Step 3 :

In both the stores A and B, find the value of "x" (no. of weeks) for y = $200 (Total money to be paid). 

The total amount $200 is completed in 7 weeks in store A and in 10 weeks in store B. 

So, store A allows Jose to pay for the game system faster.

Question 3 : 

A roller coaster park is open from May to October each year. The graph shows the number of park visitors over its season.

Answers :

(i) Segment 1 shows that attendance during the opening weeks of the park’s season stayed constant. Describe what Segment 2 shows.

A steep upward slope shows that attendance rises quickly.

(ii) Based on the time frame, give a possible explanation for the change in attendance represented by Segment 2.

The increase might coincide with summer break from school.

(iii) Which segments of the graph show decreasing attendance? Give a possible explanation.

Segments 4 and 5; the decrease might coincide with the end of summer break when school starts again.

(iv) Explain how the slope of each segment of the graph is related to whether attendance increases or decreases.

A positive slope shows that attendance increases.

A negative slope shows that attendance decreases.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.