COORDINATE GEOMETRY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Coordinate geometry, also called Analytical geometry is a branch of mathematics, in which curves in a plane are represented by algebraic equations.
For example, the equation
x2 + y2 = 1
describes a circle of unit radius in the plane. Thus coordinate geometry can be seen as a branch of mathematics which interlinks algebra and geometry, where algebraic equations are represented by geometric curves.
This connection makes it possible to reformulate problems in geometry to problems in algebra and vice versa. Thus, in coordinate geometry, the algebraic equations have visual representations thereby making our understanding much deeper.
For instance, the first degree equation in two variables
ax + by + c = 0
represents a straight line in a plane. Overall, coordinate geometry is a tool to understand concepts involved visually and created new branches of mathematics in modern times.
At the initial stage of coordinate geometry, you will study about coordinate axes, coordinate plane, plotting of points in a plane, distance between two points, section formulae, etc.
All these concepts form the basics of coordinate geometry. Let us recall some of the basic formulas.
Coordinate Plane :
The Cartesian coordinate plane is formed by two perpendicular number lines that intersect at the zeros, or the origin. The intersecting number lines divide the plane into four regions, called quadrants.
The quadrants are numbered with Roman numerals from one to four (I, II, III, IV) starting in the upper right-hand quadrant and moving counterclockwise.
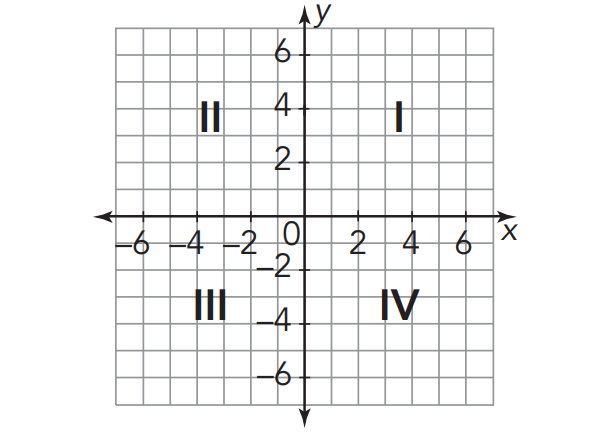
Sign of x-coordinate and y-coordinate in each quadrant :
|
Quadrant II (-x, +y) |
Quadrant I (+x, +y) |
|
Quadrant III (-x, -y) |
Quadrant IV (+x, -y) |
Distance between two points :
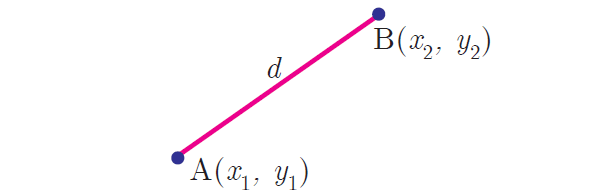
Distance between two points A(x1, y1) and B(x2, y2) is
Mid-point of line segment :
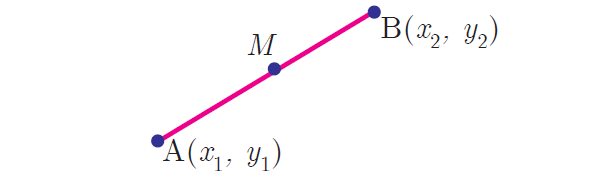
The mid-point M, of the line segment joining A(x1, y1) and B(x2, y2) is
Section Formula (Internal Division) :
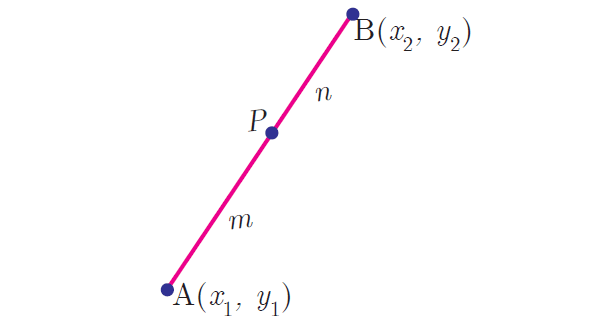
Let A(x1, y1) and B(x2, y2) be two distinct points such that point p(x, y) divides AB internally in the ratio m : n.
Then the coordinates of P are given by
Section Formula (Internal Division) :
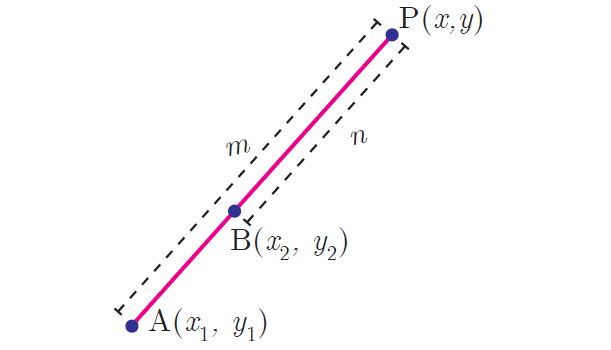
Let A(x1, y1) and B(x2, y2) be two distinct points such that point p(x, y) divides AB externally in the ratio m : n.
Then the coordinates of P are given by
Centroid of a Triangle :
The coordinates of the centroid (G) of a triangle with vertices A(x1, y1), B(x2, y2) and C(x3, y3) are given by
Area of a Triangle :
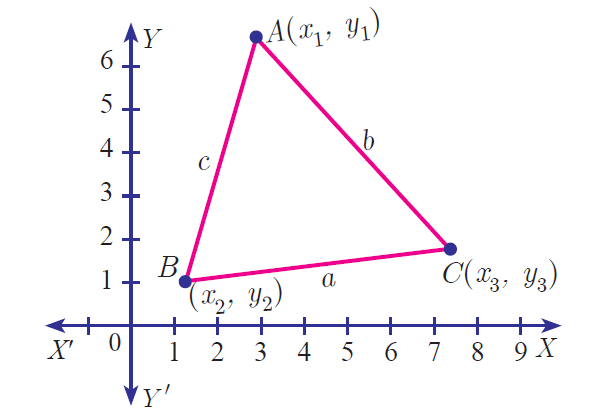
Area of a Triangle :
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of a triangle.
Then the area of ΔABC is the absolute value of the expression :
The vertices A(x1, y1), B(x2, y2) and C(x3, y3) of ΔABC are said to be “taken in order” if A, B, C are taken in counter-clock wise direction. If we do this, then area of DABC will never be negative.
Collinearity of three points :
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the three distinct points. If these three points are collinear (lie on the same straight line), then ΔABC = 0.
That is,
Area of a Quadrilateral :
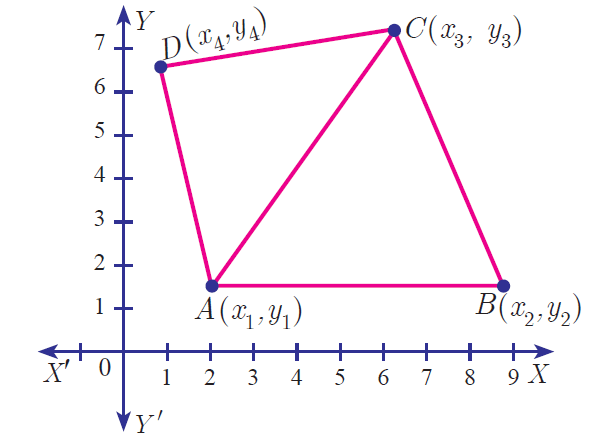
Let A(x1, y1), B(x2, y2), C(x3, y3) and D(x3, y3) be the vertices of a quadrilateral.
Then the area of quadrilateral ABCD is
Problem 1 :
ABC is an equilateral triangle is shown in the figure. Find the coordinates of its vertices.
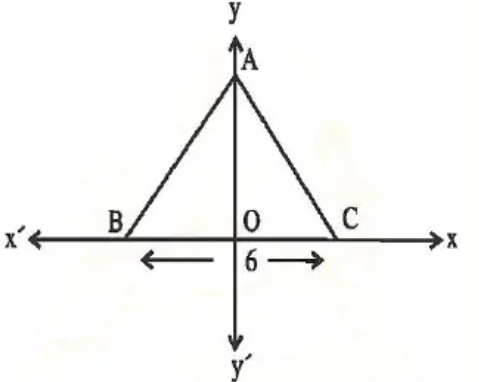
Solution :
Since triangle ABC is an equilateral triangle all sides will be equal.
AB = BC = CA
- Moving 3 units to the right, we get C. So, the point C is (3, 0)
- Moving 3 units left, we get B. So, the point B is (-3, 0)
- Moving 6 units up, we get A. So, the point A is (6, 0).
Problem 2 :
If the distance between the points (4, p) and (1, 0) is 5 units, then the value of p is
(a) 4 only (b) ± 4 (c) –4 only (d) 0
Solution :
= √(x2 - x1)2 + (y2 - y1)2
√(0 - p)2 + (1 - 4)2 = 5
√p2 + (-3)2 = 5
p2 + 9 = 52
p2 + 9 = 25
p2 = 25 - 9
p2 = 16
p = ± 4
Problem 3 :
The points (2, 5), (4, – 1) and (6, – 7) are vertices of an
(a) isosceles triangle (b) equilateral triangle
(c) right-angled triangle (d) none of these
Solution :
Let the vertices be A (2, 5), B (4, – 1) and C (6, – 7)
Length of AB = √(x2 - x1)2 + (y2 - y1)2
= √(-1 - 5)2 + (4 - 2)2
= √(-6)2 + 22
= √(36 + 4)
= √40
= 2√10
Length of BC = √(-7 + 1)2 + (6 - 4)2
= √(-6)2 + 22
= √(36 + 4)
= √40
= 2√10
Length of CA = √(-7 - 5)2 + (6 - 2)2
= √(-12)2 + 42
= √(144 + 16)
= √160
= 4√10
Since two sides are equal, it must be isosceles triangle. Option a is correct.
Problem 4 :
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Solution :
In a parallelogram, the midpoint of the diagonal will be equal.
Midpoint of diagonal AC = (x1 + x2)/2, (y1 + y2)/2
= (3 + a)/2, (1 + b)/2 ------(1)
Midpoint of diagonal BD = (5 + 4)/2, (1 + 3)/2
= 9/2, 4/2
= (9/2, 2) ----------(2)
(1) = (2)
|
(3 + a)/2 = 9/2 3 + a = 9 a = 9 - 3 a = 6 |
(1 + b)/2 = 2 1 + b = 4 b = 4 - 1 b = 3 |
So, the required point is (6, 3).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problems on Exponents and Radicals
Feb 21, 26 08:28 PM
SAT Math Problems on Exponents and Radicals -
SAT Math Problems on Angles
Feb 21, 26 08:20 PM
SAT Math Problems on Angles -
Digital SAT Math Problems and Solutions (Part - 9)
Feb 21, 26 10:41 AM
Digital SAT Math Problems and Solutions (Part - 9)

