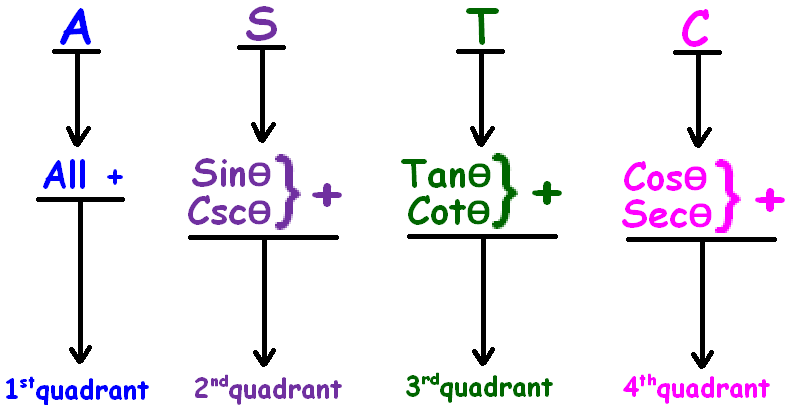
ALL STUDENTS TAKE CALCULUS
About "All Students Take Calculus"
"All Students Take Calculus"
or
"All Students Take Coffee"
or
"All Sliver Tea Cups"
is the way to remember ASTC formula in trigonometry.
ASTC formula helps us to evaluate different trigonometric ratios in different quadrants.
"All Students take calculus" rule or ASTC formula has been explained clearly in the figure given below.
More clearly
In the first quadrant (0° to 90°), all trigonometric ratios are positive.
In the second quadrant (90° to 180°), sin and csc are positive and other trigonometric ratios are negative.
In the third quadrant (180° to 270°), tan and cot are positive and other trigonometric ratios are negative.
In the fourth quadrant (270° to 360°), cos and sec are positive and other trigonometric ratios are negative.
Important conversions
When we have the angles 90° and 270° in the trigonometric ratios in the form of
(90° + θ)
(90° - θ)
(270° + θ)
(270° - θ)
We have to do the following conversions,
sin θ <------> cos θ
tan θ <------> cot θ
csc θ <------> sec θ
For example,
sin (270° + θ) = - cos θ
cos (90° - θ) = sin θ
For the angles 0° or 360° and 180°, we should not make the above conversions.
Division of Quadrants
(90° - θ) -------> I st Quadrant
(90° + θ) and (180° - θ) -------> II nd Quadrant
(180° + θ) and (270° - θ) -------> III rd Quadrant
(270° + θ), (360° - θ) and (- θ) -------> IV th Quadrant
Evaluation of trigonometric ratios using "All students take calculus" rule
Let us see, how to use ASTC formula.
Example 1 :
Evaluate : cos (270° - θ)
Solution :
To evaluate cos (270° - θ), we have to consider the following important points.
(i) (270° - θ) will fall in the III rd quadrant.
(ii) When we have 270°, "cos" will become "sin"
(iii) In the III rd quadrant, the sign of "cos" is negative.
Considering the above points, we have
cos (270° - θ) = - sin θ
Example 2 :
Evaluate : sin (180° + θ)
Solution :
To evaluate sin (180° + θ), we have to consider the following important points.
(i) (180° + θ) will fall in the III rd quadrant.
(ii) When we have 180°, "sin" will not be changed
(iii) In the III rd quadrant, the sign of "sin" is negative.
Considering the above points, we have
sin (180° + θ) = - sin θ
Based on the above two examples, we can evaluate the following trigonometric ratios.
|
sin (-θ) = - sin θ cos (-θ) = cos θ tan (-θ) = - tan θ csc (-θ) = - csc θ sec (-θ) = sec θ cot (-θ) = - cot θ sin (90°-θ) = cos θ cos (90°-θ) = sin θ tan (90°-θ) = cot θ csc (90°-θ) = sec θ sec (90°-θ) = csc θ cot (90°-θ) = tan θ sin (90°+θ) = cos θ cos (90°+θ) = -sin θ tan (90°+θ) = -cot θ csc (90°+θ) = sec θ sec (90°+θ) = -csc θ cot (90°+θ) = -tan θ sin (180°-θ) = sin θ cos (180°-θ) = -cos θ tan (180°-θ) = -tan θ |
csc (180°-θ) = csc θ sec (180°-θ) = -sec θ cot (180°-θ) = -cot θ sin (180°+θ) = -sin θ cos (180°+θ) = -cos θ tan (180°+θ) = tan θ csc (180°+θ) = -csc θ sec (180°+θ) = -sec θ csc (180°+θ) = cot θ sin (270°-θ) = -cos θ cos (270°-θ) = -sin θ tan (270°-θ) = cot θ csc (270°-θ) = -sec θ sec (270°-θ) = -csc θ cot (270°-θ) = tan θ sin (270°+θ) = -cos θ cos (270°+θ) = sin θ tan (270°+θ) = -cot θ csc (270°+θ) = -sec θ sec (270°+θ) = cos θ cot (270°+θ) = -tan θ |
Angles greater than or equal to 360°
If the angle is equal to or greater than 360°, we have to divide the given angle by 360 and take the remainder.
For example,
(i) Let us consider the angle 450°.
When we divide 450° by 360, we get the remainder 90°.
Therefore, 450° = 90°
(ii) Let us consider the angle 360°
When we divide 360° by 360, we get the remainder 0°.
Therefore, 360° = 0°
Based on the above two examples, we can evaluate the following trigonometric ratios.
sin (360° - θ) = sin (0° - θ) = sin (- θ) = - sin θ
cos (360° - θ) = cos (0° - θ) = cos (- θ) = cos θ
tan (360° - θ) = tan (0° - θ) = tan (- θ) = - tan θ
csc (360° - θ) = csc (0° - θ) = csc (- θ) = - csc θ
sec (360° - θ) = sec (0° - θ) = sec (- θ) = sec θ
cot (360° - θ) = cot (0° - θ) = cot (- θ) = - cot θ
All students take calculus - Practice problems
Problem 1 :
Evaluate : tan 735°
Solution :
The given 735° is greater than 360°.
So, we have to divide 735° by 360 and take the remainder.
When 735° is divided by 360, the remainder is 15°.
Therefore,
735° = 15° ------> tan 735° = tan 15°
Hence, tan 735° is equal to tan 15°
Let us look at the next problem on "All students take calculus"
Problem 2 :
Evaluate : cos (-870°)
Solution :
Since the given angle (-870°) has negative sign, we have to assume it falls in the fourth quadrant.
In the fourth quadrant, "cos" is positive.
So, we have cos (-870°) = cos 870°.
The given 870° is greater than 360°.
So, we have to divide 870° by 360 and take the remainder.
When 870° is divided by 360, the remainder is 150°.
Therefore,
870° = 150° ------> cos 870° = cos 150°
cos 870° = cos (180° - 30°)
cos 870° = - cos 30°
cos 870 = - √3 / 2
Hence, cos 870° is equal to - √3 / 2 .
Let us look at the next problem on "All students take calculus"
Problem 3 :
Find the value of (sin 780 sin 480° + cos 120° cos 60°)
Solution :
Let us find the value of each trigonometric ratio for the given angle.
sin 780° = sin 60° = √3 / 2
sin 480° = sin 120° = sin (180° - 60°) = sin 60° = √3 / 2
cos 120° = cos (180° - 60°) = - cos 60° = - 1 / 2
cos 60° = 1/2
sin780 sin480° + cos120° cos60° = (√3/2) x (√3/2) + (-1/2) x (1/2)
= (3/4) - (1/4)
= (3-1) / 4
= 2 / 4
= 1/2
Hence, the value of the given trigonometric expression is equal to 1/2.
Let us look at the next problem on "All students take calculus"
Problem 4 :
Simplify :
cot (90°-θ) sin (180°+θ) sec(360°-θ) / tan(180°+θ) sec(-θ) cos(90°+θ)
Solution :
Using ASTC formula, we have
cot (90°-θ) = tan θ
sin (180°+θ) = - sin θ
sec(360°-θ) = sec θ
tan(180°+θ) = tan θ
sec(-θ) = sec θ
cos(90°+θ) = - sin θ
The given expression is
= (tan θ x -sinθ x sec θ) / (tan θ x sec θ x -sin θ)
= 1
Hence, the simplification of the given trigonometric expression is equal to 1.
Let us look at the next problem on "All students take calculus"
Problem 5 :
Simplify :
sec(360°-θ) tan(180°-θ) + cot(90°+θ) co(270°-θ)
Solution :
Using ASTC formula, we have
sec (360°-θ) = sec θ
tan (180°-θ) = - tan θ
cot (90°+θ) = - tan θ
cos (270°-θ) = - sec θ
The given expression is
= sec θ x (-tan θ) + (-tan θ) x (-sec θ)
= - sec θ x tan θ + sec θ x tan θ
= 0
Hence, the simplification of the given trigonometric expression is equal to 0.
After having gone through the stuff given above, we hope that the students would have understood "All students take calculus" rule
If you want to know more about "All students take calculus" rule, please click here
Apart from "All students take calculus" rule, if you need any other stuff in math, please use our google custom search here.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
