ALGEBRAIC REPRESENTATIONS OF ROTATIONS

To rotate a figure in the coordinate plane, rotate each of its vertices. Then connect the vertices to form the image.

We can use the rules shown in the table for changing the signs of the coordinates after a reflection about the origin.

Example 1 :

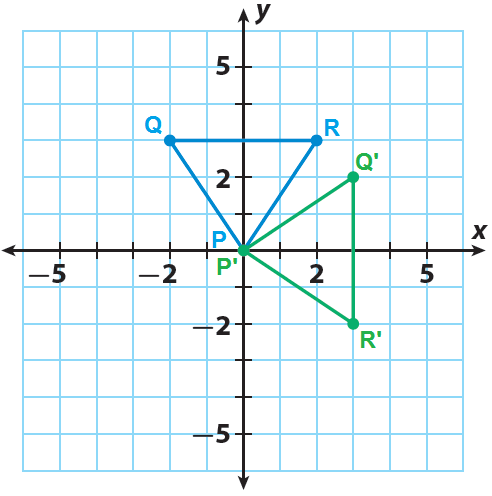
The triangle PQR has the following vertices P(0, 0), Q(-2, 3) and R(2,3). Rotate the triangle PQR 90° clockwise about the origin.

Solution :

Step 1 :

Trace triangle PQR and the x- and y-axes onto a piece of paper.

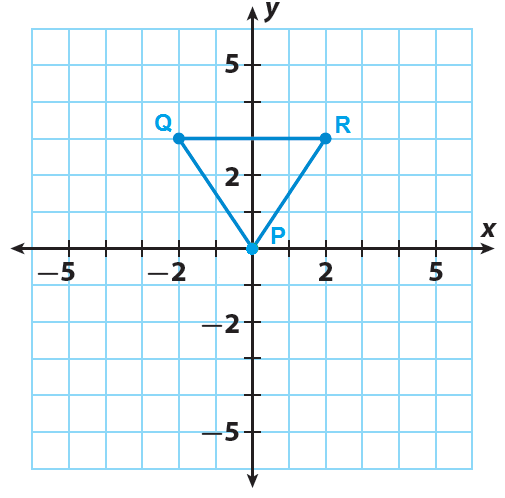
Step 2 :

Let P', Q' and R' be the vertices of the rotated figure.

Since the triangle is rotated 90° clockwise about the origin, the rule is

(x, y) ----> (y, -x)

Step 3 :

P(0, 0) ----> P'(0, 0)

Q(-2, 3) ----> Q'(3, 2)

R(2, 3) ----> R'(3, -2)

Step 4 :

Sketch the image P'Q'R' using the points P'(0, 0), Q'(3, 2) and  Z'(3, -2).

Example 2 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° counterclockwise about the origin.

Solution :

Step 1 :

Trace triangle XYZ and the x- and y-axes onto a piece of paper.

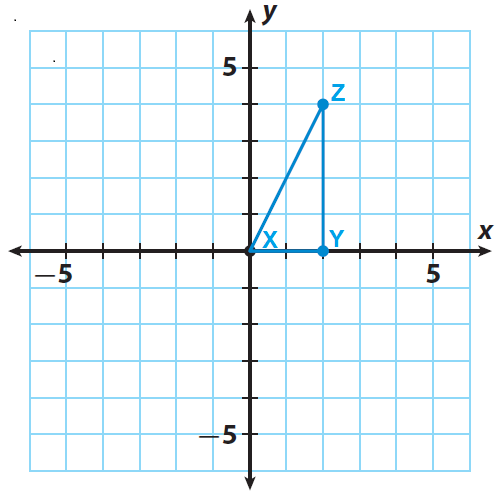
Step 2 :

Let X', Y' and Z' be the vertices of the rotated figure.

Since the triangle is rotated 90° counterclockwise about the origin, the rule is

(x, y) ----> (-y, x)

Step 3 :

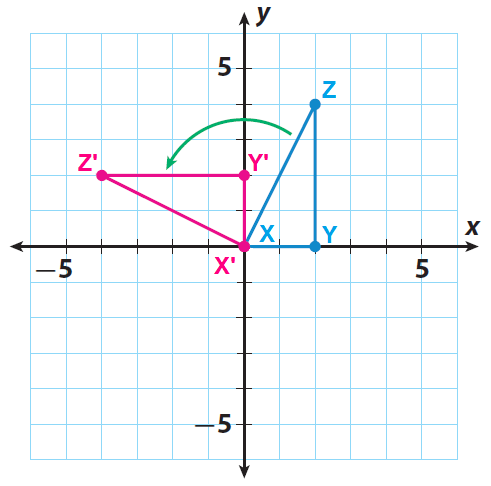
X(0, 0) ----> X'(0, 0)

Y(2, 0) ----> Y'(0, 2)

Z(2, 4) ----> Z'(-4, 2)

Step 4 :

Sketch the image X'Y'Z' using the points X'(0, 0), Y'(0, 2) and  Z'(-4, 2).

Example 3 :

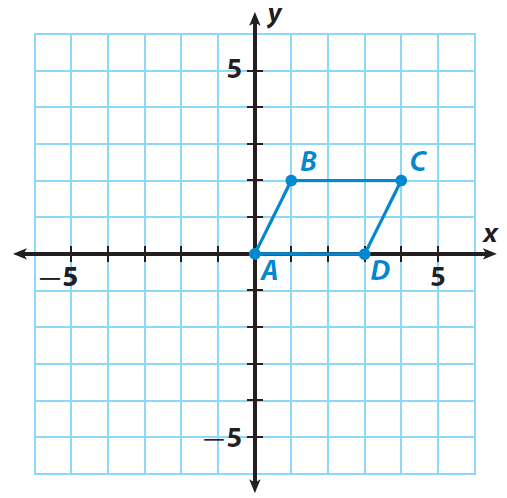
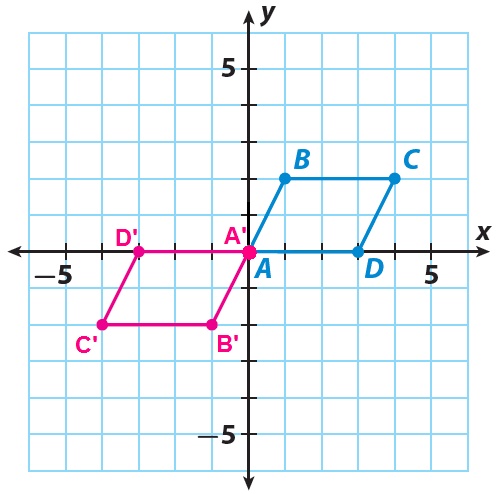
A quadrilateral has the following vertices A(0, 0), B(1, 2), C(4, 2) and D(3, 0). Rotate the quadrilateral 180° clockwise about the origin.

Solution :

Step 1 :

Trace the quadrilateral ABCD and the x- and y-axes onto a piece of paper.

Step 2 :

Let A', B', C' and D' be the vertices of the rotated figure.

Since the quadrilateral is rotated 180° clockwise about the origin, the rule is

(x, y) ----> (-x, -y)

Step 3 :

A(0, 0) ----> A'(0, 0)

B(1, 2) ----> B'(-1, -2)

C(4, 2) ----> C'(-4, -2)

D(3, 0) ----> D'(-3, 0)

Step 4 :

Sketch the image A'B'C'D' using the points A'(0, 0), B'(-1, -2), C(-4, -2) and  D'(-3, 0).

Example 4 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 270° counterclockwise about the origin.

Solution :

Step 1 :

Trace triangle XYZ and the x- and y-axes onto a piece of paper.

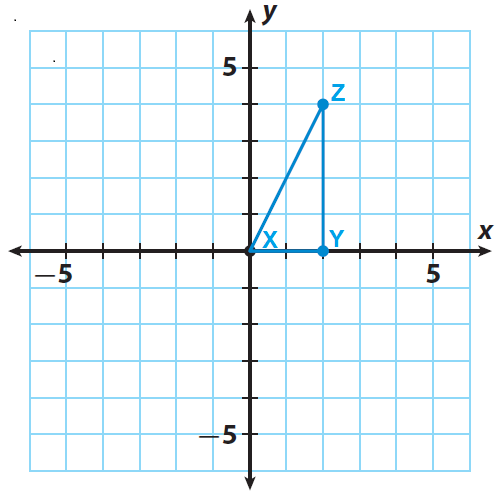
Step 2 :

Let X", Y" and Z" be the vertices of the rotated figure.

Since the triangle is rotated 270° counterclockwise about the origin, the rule is

(x, y) ----> (y, -x)

Step 3 :

X(0, 0) ----> X"(0, 0)

Y(2, 0) ----> Y"(0, -2)

Z(2, 4) ----> Z"(4, -2)

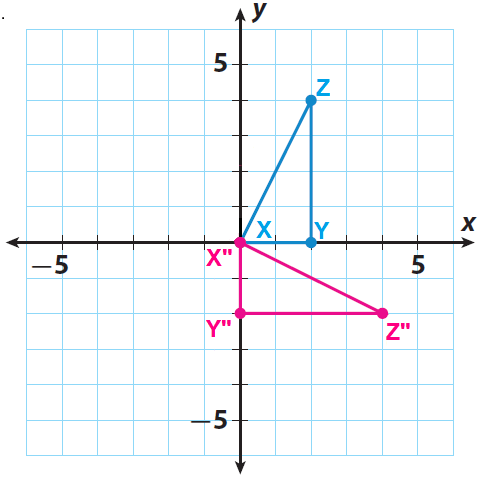
Step 4 :

Sketch the image X"Y"Z" using the points X"(0, 0),  Y"(0, -2) and  Z"(4, -2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.