ALGEBRAIC REPRESENTATIONS OF REFLECTIONS

To reflect a figure across a line of reflection, reflect each of its vertices. Then connect the vertices to form the image. Each point and its image must be at the same distance from the line of reflection.

We can use the rules shown in the table for changing the signs of the coordinates after a reflection.

Example 1 :

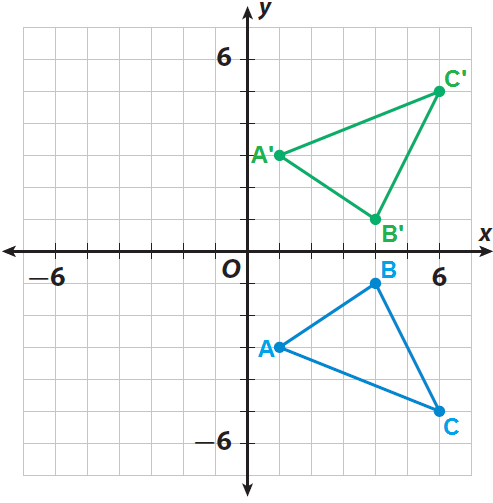
Triangle ABC has the vertices A(1, -3), B(4, -1) and C(6, -5). Find the vertices of triangle A'B'C' after a reflection across the x-axis. Then graph the triangle and its image.

Solution :

Step 1 :

Apply the rule to find the vertices of the image.

Since there is a reflection across the x-axis, we have to multiply each y-coordinate by -1.

That is, (x, y) ----> (x, -y).

Step 2 :

A(1, -3) ----> A'(1, 3)

B(4, -1) ----> B'(4, 1)

C(6, -5) ----> C'(6, 5)

Step 3 :

Graph the triangle ABC and its image.

Example 2 :

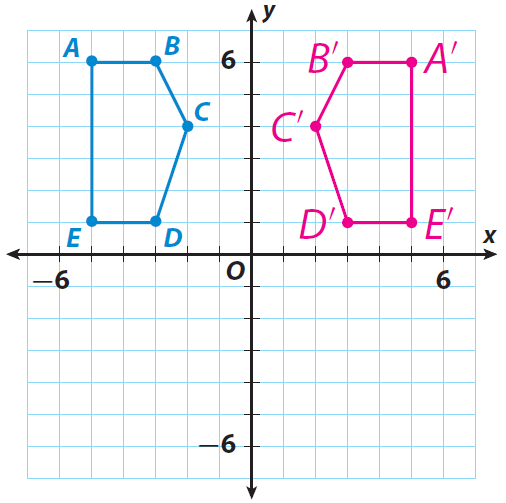
A pentagon has the vertices A(-5, 6), B(-3, 6), C(-2, 4), D(-3, 1) and E(-5,1). Find the vertices of the pentagon A'B'C'D'E' after a reflection across the y-axis. Then graph the pentagon and its image.

Solution :

Step 1 :

Apply the rule to find the vertices of the image.

Since there is a reflection across the y-axis, we have to multiply each x-coordinate by -1.

That is, (x, y) ----> (-x, y).

Step 2 :

A(-5, 6) ----> A'(5, 6)

B(-3, 6) ----> B'(3, 6)

C(-2, 4) ----> C'(2, 4)

D(-3, 1) ----> D'(3, 1)

E(-5, 1) ----> E'(5, 1)

Step 3 :

Graph the pentagon ABCDE and its image.

Example 3 :

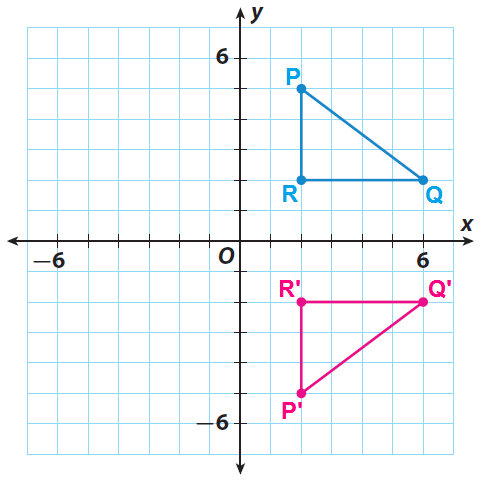
Triangle PQR has the vertices P(2, 5), Q(6, 2) and R(2, 2). Find the vertices of triangle P'Q'R' after a reflection across the x-axis. Then graph the triangle and its image.

Solution :

Step 1 :

Apply the rule to find the vertices of the image.

Since there is a reflection across the x-axis, we have to multiply each y-coordinate by -1.

That is, (x, y) ----> (x, -y).

Step 2 :

P(2, 5) ----> P'(2, -5)

Q(6, 2) ----> Q'(6, -2)

R(2, 2) ----> R'(2, -2)

Step 3 :

Graph the triangle PQR and its image.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.