ALGEBRAIC REPRESENTATIONS OF DILATIONS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
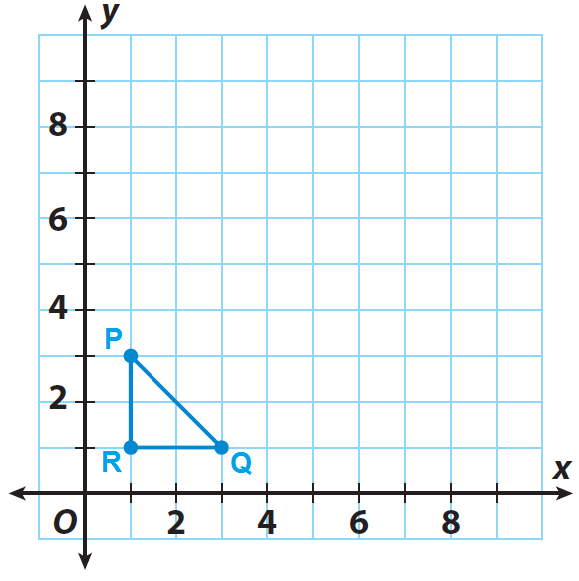
Problem 1 :
The triangle PQR shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 3, graph the dilated image P'Q'R'.
Problem 2 :
The triangle ABC shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 1/3, graph the dilated image A'B'C'.
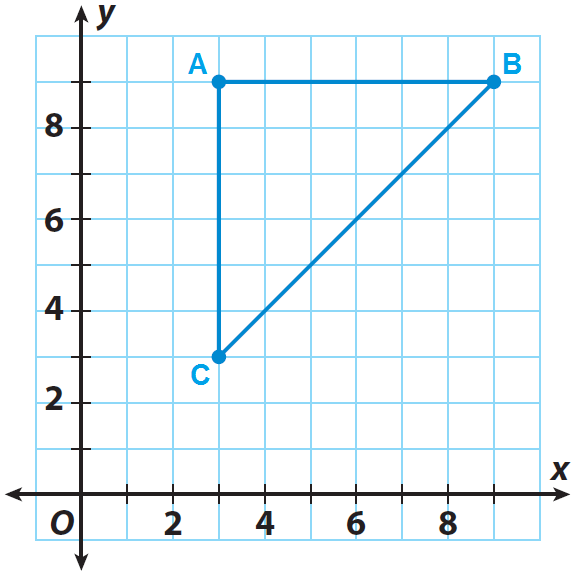
Problem 3 :
The arrow ABCDE shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 0.5, graph the dilated image A'B'C'D'E'.
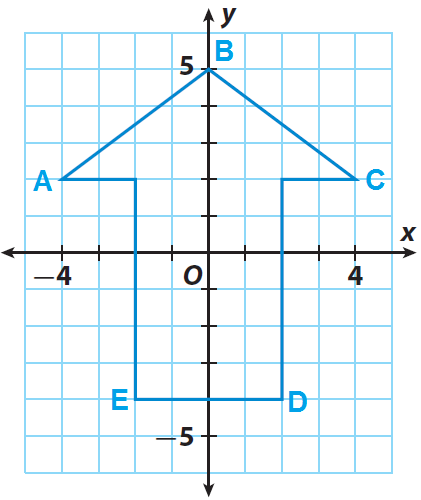
Problem 4 :
The rectangle JKLM shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 2, graph the dilated image J'K'L'M'.
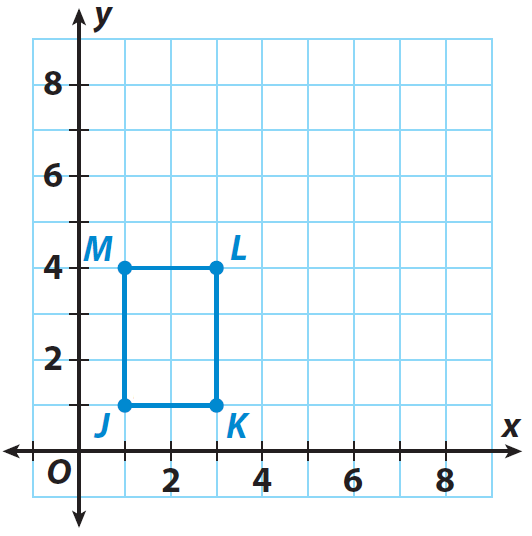

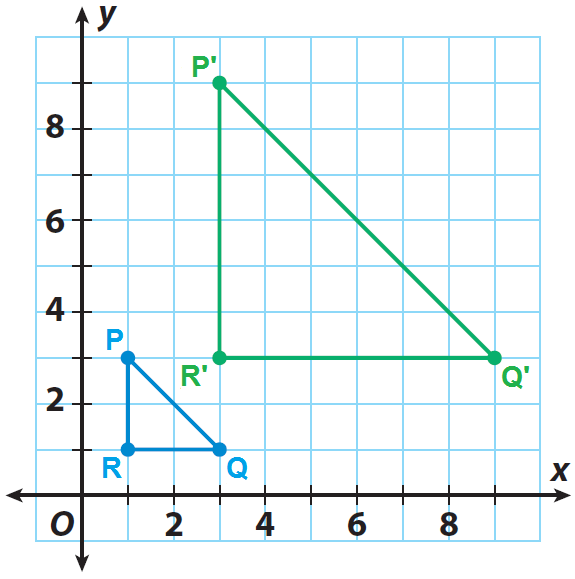
1. Answer :

Step 1 :
List the coordinates of the vertices of the pre image.
P(1, 3), Q(3, 1) and R(1, 1)
Step 2 :
Since the scale factor is 3, the rule to get the coordinates of the vertices of the image is
(x, y) ----> (3x, 3y)
Step 3 :
List the coordinates of the vertices of the image.
P(1, 3) ----> P'(3, 9)
Q(3, 1) ----> Q'(9, 3)
R(1, 1) ----> R'(3, 3)
Step 4 :
Graph the image P'Q'R'.
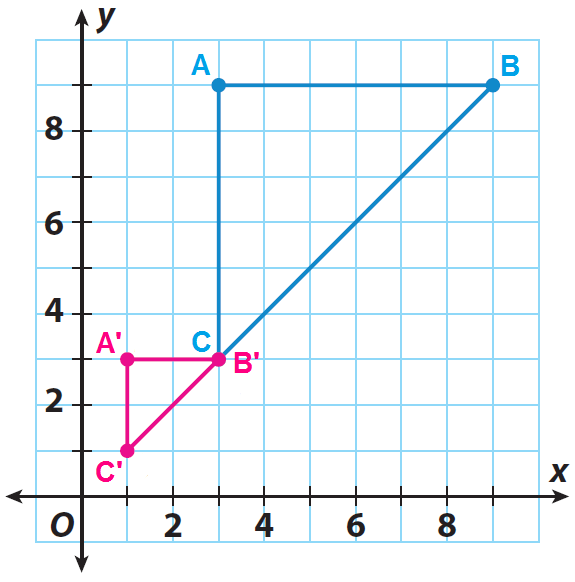
2. Answer :

Step 1 :
List the coordinates of the vertices of the pre image.
A(3, 9), B(9, 9) and C(3, 3)
Step 2 :
Since the scale factor is 1/3, the rule to get the coordinates of the vertices of the image is
(x, y) → [(1/3)x, (1/3)y]
Step 3 :
List the coordinates of the vertices of the image.
A(3, 9) ----> A'(1, 3)
B(9, 9) ----> B'(3, 3)
C(3, 3) ----> C'(1, 1)
Step 4 :
Graph the image A'B'C'.
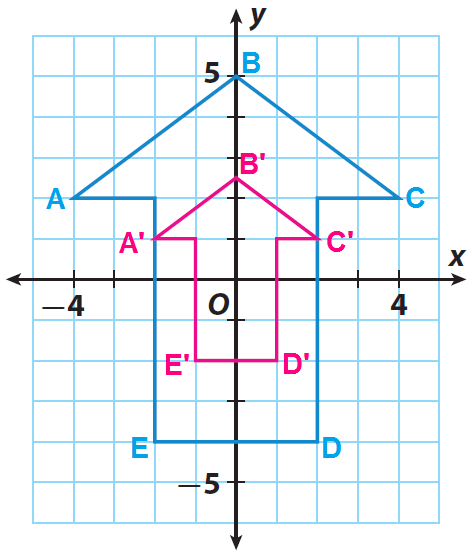
3. Answer :

Step 1 :
List the coordinates of the vertices of the pre image.
A(1, 1), B(3, 1), C(3, 4), D(1, 4) and E(2, 3)
Step 2 :
Since the scale factor is 1/2, the rule to get the coordinates of the vertices of the image is
(x, y) ----> [0.5x, 0.5y]
Step 3 :
List the coordinates of the vertices of the image.
A(-4, 2) ----> A'(-2, 1)
B(0, 5) ----> B'(0, 2.5)
C(4, 2) ----> C'(2, 1)
D(2, -4) ----> D'(1, -2)
E(-2, -4) ----> E'(-1, -2)
Step 4 :
Graph the image A'B'C'D'E'.
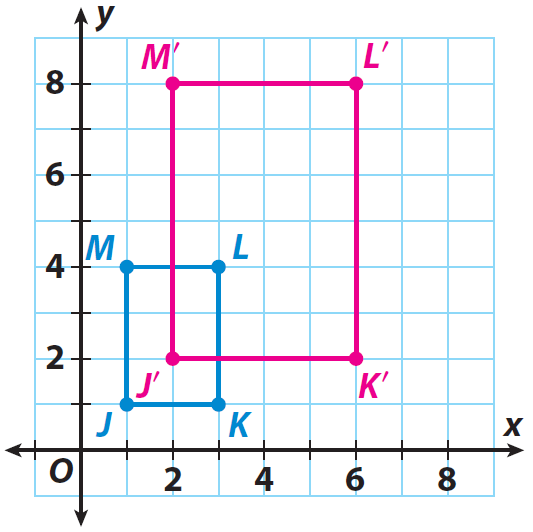
4. Answer :
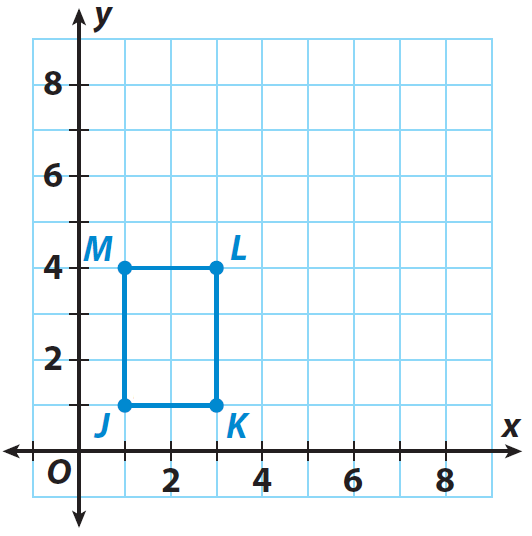
Step 1 :
List the coordinates of the vertices of the pre image.
J(1, 1), K(3, 1), L(3, 4) and M(1, 4)
Step 2 :
Since the scale factor is 2, the rule to get the coordinates of the vertices of the image is
(x, y) ----> (2x, 2y)
Step 3 :
List the coordinates of the vertices of the image.
J(1, 1) ----> J'(2, 2)
K(3, 1) ----> K'(6, 2)
L(3, 4) ----> L'(6, 8)
M(1, 4) ----> M'(2, 8)
Step 4 :
Graph the image J'K'L'M'.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
