ALGEBRA AND ANGLE MEASURES

Algebra can be used to find unknown values in angles using appropriate theorems and postulates in geometry. 

Example 1 :

If m∠1 = 3x + 15, m∠2 = 4x - 5, and m∠3 = 5y, find the value of x and y.

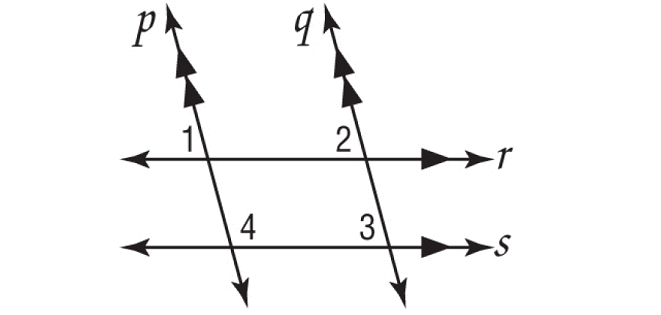
Solution : 

m∠1 and m∠2 are corresponding angles and they are equal.

m∠1  =  m∠2

3x + 15  =  4x - 5

Subtract 3x from each side. 

15  =  x - 5

Add 5 to each side. 

20  =  x

m∠2 and m∠3 are corresponding angles and they are equal.

m∠2  =  m∠3

4x - 5  =  5y

Substitute x = 20.

4(20) - 5  =  5y

80 - 5  =  5y

75  =  5y

Divide each side by 5.

15  =  y

Therefore, 

x  =  20  and  y  =  15

Example 2 :

In the figure shown below, find the values of x and y.

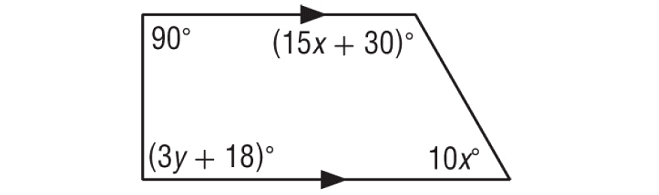
Solution : 

(3y + 18)° and 90° are interior angles on the same side of the transversal and they are supplementary. 

(3y + 18)° + 90°  =  180°

3y + 18 + 90  =  180

3y + 108  =  180

Subtract 108 from each side. 

3y  =  72

Divide each side by 3.

y  =  24

10x° and (15x + 30)° are interior angles on the same side of the transversal and they are supplementary. 

10x° + (15x + 30)°  =  180°

10x + 15x + 30  =  180

25x + 30  =  180

Subtract 180 from each side. 

25x  =  150

Divide each side by 25.

x  =  6

Therefore, 

x  =  6  and  y  =  24

Example 3 :

In the figure shown below, find the values of x, y and z.

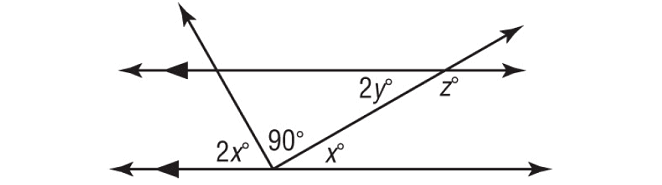
Solution : 

2x°, 90° and x° together form a straight angle. 

2x° + 90° + x°  =  180°

3x + 90  =  180

Subtract 90 from each side. 

3x  =  90

Divide each side by 3.

x  =  30

x° and 2y° are alternate interior angles and they are equal. 

2y°  =  x°

2y  =  x

Substitute x = 30.

2y  =  30

Divide each side by 2.

y  =  15

2y° and z° form a linear pair, they are supplementary. 

2y° + z°  =  180°

2y + z  =  180

Substitute y = 15. 

2(15) + z  =  180

30 + z  =  180

Subtract 30 from each side. 

z  =  150

Therefore, 

x  =  30, y  =  15  and  z  =  150

Example 4 :

In the figure shown below, find the values of x and y.

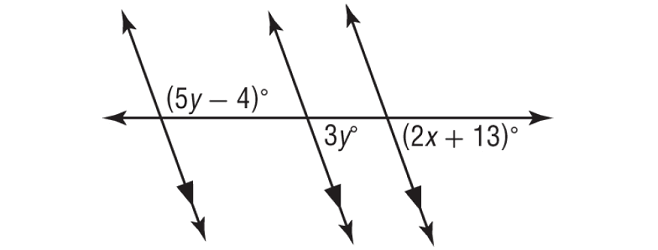
Solution : 

Mark a new angle a°. 

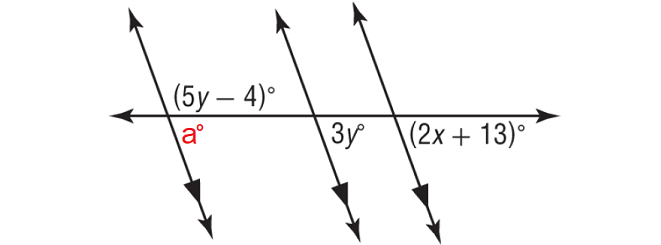
a° and (5y - 4)° form a linear pair. 

a° + (5y - 4)°  =  180°

a° and 3y° are corresponding angles, then  a° = 3y°.

3y° + (5y - 4)°  =  180°

3y + 5y - 4  =  180

8y - 4  =  180

Add 4 to each side. 

8y  =  184

Divide each side by 8.

y  =  23

3y° and (2x + 13)° are corresponding angles and they are equal.

(2x + 13)°  =  3y°

2x + 13  =  3y

Substitute y = 23. 

2x + 13  =  3(23)

2x + 13  =  69

Subtract 13 from each side. 

2x  =  56

Divide each side by 2.

x  =  28

Example 5 :

Using a 3^rd parallel Line – Auxiliary Line, find the value of x. 

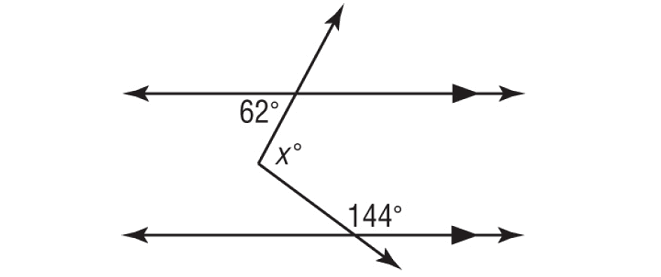
Solution :

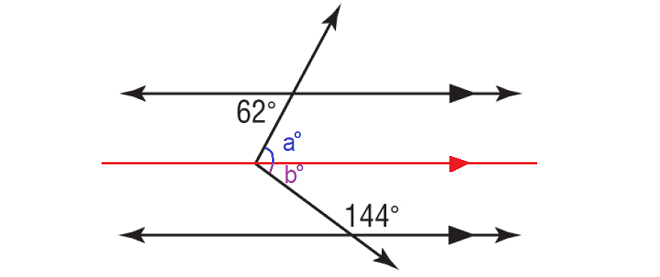
In the figure above, a° and 62° are alternate interior angles and they are equal.

a°  =  62°

b° and 144° are interior angles on the same side of the transversal and they are supplementary. 

b° + 144°  =  180°

Subtract 144° from each side. 

b°  =  36°

In the above figure, 

x  =  a + b

=  62 + 36

=  98

Example 6 :

In the figure shown below, find the values of x and y.

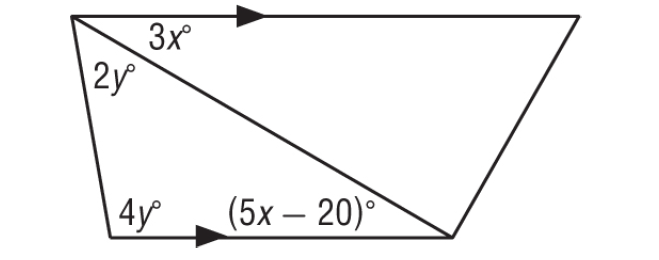
Solution : 

3x° and (5x - 20)° are alternate interior angles and they are equal. 

3x°  =  (5x - 20)°

3x  =  5x - 20

Subtract 3x from each side. 

0  =  2x - 20

Add 20 to each side. 

20  =  2x

Divide each side by 2.

10  =  x

By Triangle Angle Sum Theorem, 

(5x - 20)° + 2y° + 4y°  =  180°

5x - 20 + 2y + 4y  =  180

5x - 20 + 6y  =  180

Substitute x = 10.

5(10) - 20 + 6y  =  180

50 - 20 + 6y  =  180

30 + 6y  =  180

Subtract 30 from each side. 

6y  =  150

Divide each side by 6.

y  =  25

Therefore, 

x  =  10  and  y  =  25

Example 7 :

In the figure shown below, find the value of x.

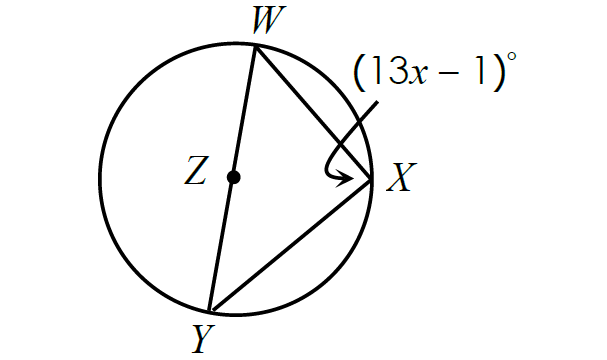
Solution : 

Since the inscribed angle ∠WXY intercepts the diameter, it is a right angle.  

m∠WXY  =  90°

(13x - 1)°  =  90°

13x - 1  =  90

Add 1 to each side. 

13x  =  91

Divide each side by 13.

x  =  7

Example 8 :

In the figure shown below, find the value of x.

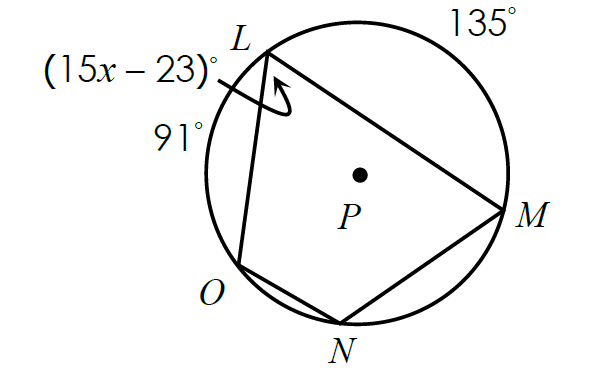
Solution : 

The measure of an inscribed angle is equal to half of the measure of its intercepted arc.

m∠ONM  =  (1/2) ⋅ m∠arc OLM

m∠ONM  =  (1/2) ⋅ (91° + 135°)

m∠ONM  =  (1/2) ⋅ 226°

m∠ONM  =  113°

Since the quadrilateral LMNO is inscribed in a circle, its opposite angles are supplementary. 

m∠OLM + m∠ONM  =  180°

Substitute.

(15x - 23)° + 113°  =  180°

15x - 23 + 113  =  180

15x + 90  =  180

Subtract 90 from each side.

15x  =  90

Divide each side by 15.

x  =  6

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.