ALGEBRA AND ANGLE MEASURES WORKSHEET

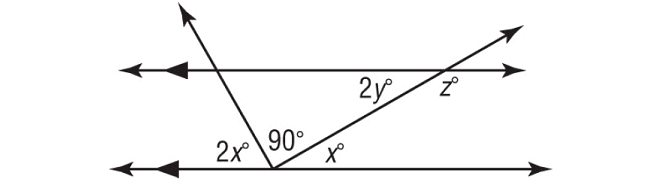
Problem 1 :

Find the values of x, y and z.

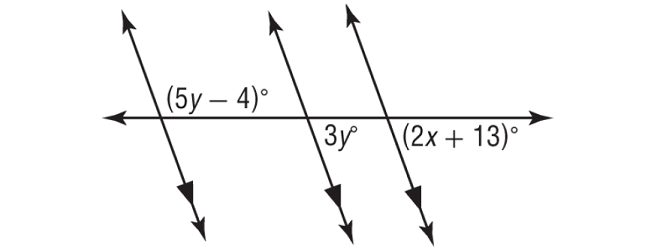
Problem 2 :

Find the values of x and y.

Problem 3 :

Using a 3^rd parallel Line – Auxiliary Line, find the value of x. 

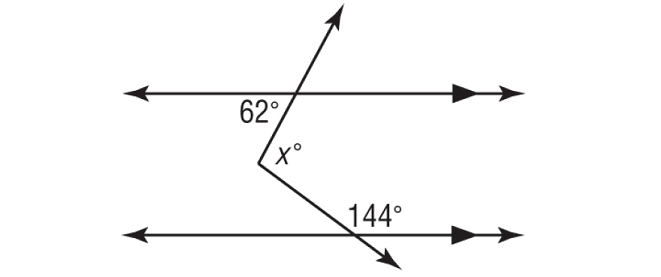
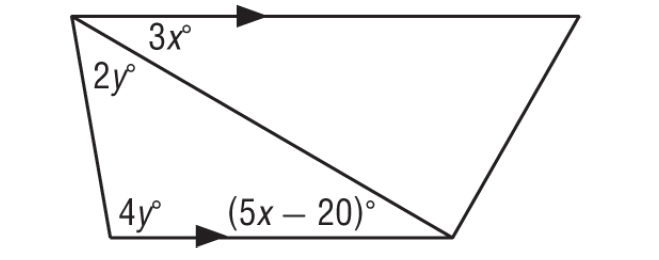
Problem 4 :

Find the values of x and y.

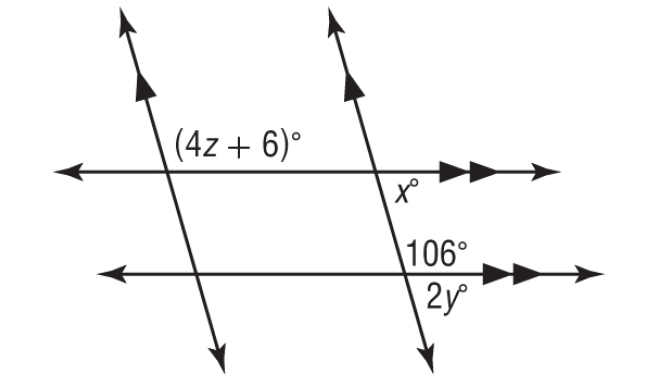
Problem 5 :

Find the values of x, y and z.

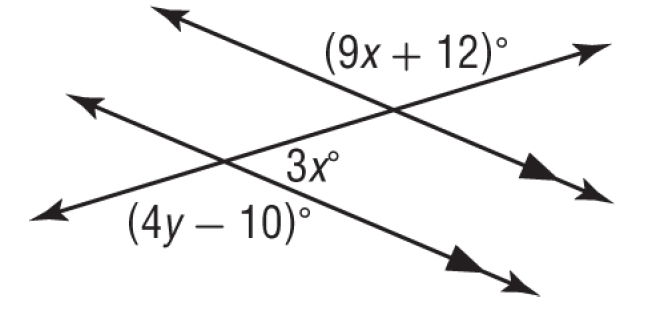
Problem 6 :

Find the values of x and y.

Problem 7 :

Solve for x.

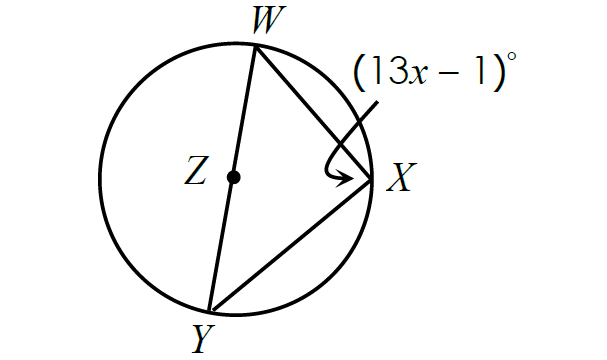
Problem 8 :

Solve for x.

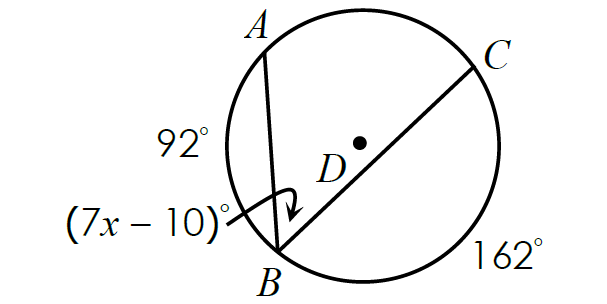
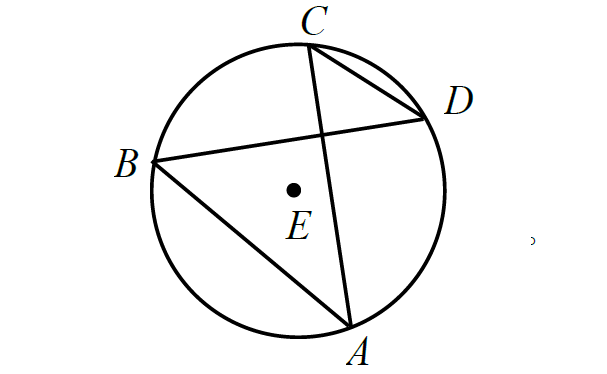
Problem 9 :

If m∠ABD = (6x + 26)° and m∠ACD = (13x – 9)°, find the value of x. 

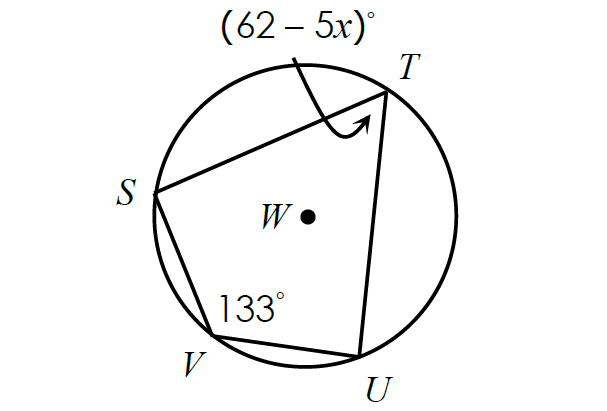
Problem 10 :

Solve for x. 

1. Answer : 

2x°, 90° and x° together form a straight angle. 

2x° + 90° + x°  =  180°

3x + 90  =  180

Subtract 90 from each side. 

3x  =  90

Divide each side by 3.

x  =  30

x° and 2y° are alternate interior angles and they are equal. 

2y°  =  x°

2y  =  x

Substitute x = 30.

2y  =  30

Divide each side by 2.

y  =  15

Therefore, 

x  =  30  and  y  =  15

2. Answer : 

Mark a new angle a°. 

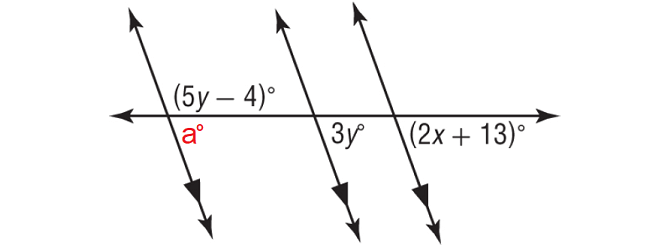
a° and (5y - 4)° form a linear pair. 

a° + (5y - 4)°  =  180°

a° and 3y° are corresponding angles, then  a° = 3y°.

3y° + (5y - 4)°  =  180°

3y + 5y - 4  =  180

8y - 4  =  180

Add 4 to each side. 

8y  =  184

Divide each side by 8.

y  =  23

3y° and (2x + 13)° are corresponding angles and they are equal.

(2x + 13)°  =  3y°

2x + 13  =  3y

Substitute y = 23. 

2x + 13  =  3(23)

2x + 13  =  69

Subtract 13 from each side. 

2x  =  56

Divide each side by 2.

x  =  28

3. Answer :

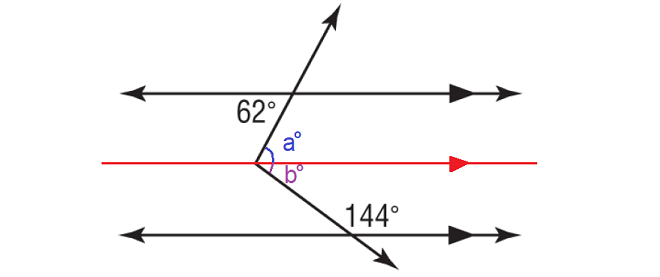
In the figure above, a° and 62° are alternate interior angles and they are equal.

a°  =  62°

b° and 144° are interior angles on the same side of the transversal and they are supplementary. 

b° + 144°  =  180°

Subtract 144° from each side. 

b°  =  36°

In the above figure, 

x  =  a + b

=  62 + 36

=  98

4. Answer : 

3x° and (5x - 20)° are alternate interior angles and they are equal. 

3x°  =  (5x - 20)°

3x  =  5x - 20

Subtract 3x from each side. 

0  =  2x - 20

Add 20 to each side. 

20  =  2x

Divide each side by 2.

10  =  x

By Triangle Angle Sum Theorem, 

(5x - 20)° + 2y° + 4y°  =  180°

5x - 20 + 2y + 4y  =  180

5x - 20 + 6y  =  180

Substitute x = 10.

5(10) - 20 + 6y  =  180

50 - 20 + 6y  =  180

30 + 6y  =  180

Subtract 30 from each side. 

6y  =  150

Divide each side by 6.

y  =  25

Therefore, 

x  =  10  and  y  =  25

5. Answer :

2y° and 106° form a linear pair, they are supplementary. 

2y° + 106°  =  180°

2y + 106  =  180

Subtract 106 from each side. 

2y  =  74

Divide each side by 2.

y  =  37

x° and 2y° are corresponding angles, they are equal. 

x°  =  2y°

x  =  2y

Substitute x = 37.

x  =  2(37)

x  =  74

Using Vertical angles Theorem, mark the angle x°. 

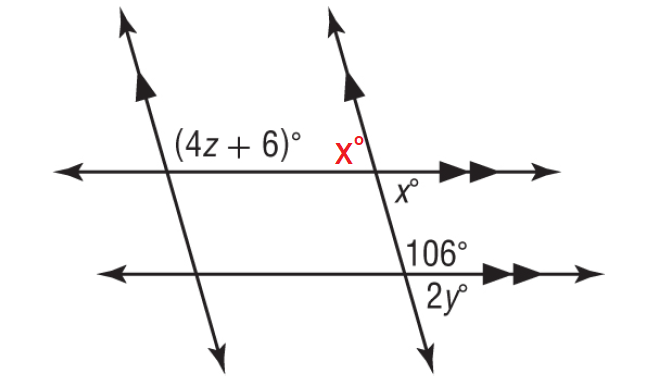
In the figure above, (4z + 6)° and x° are consecutive interior angles, they are supplementary.

(4z + 6)° + x°  =  180°

4z + 6 + x  =  180

Substitute x = 74.

4z + 6 + 74  =  180

4z + 80  =  180

Subtract 80 from each side. 

4z  =  100

Divide each side by 4.

z  =  25

Therefore, 

x  =  74, y  =  37  and  z  =  25

6. Answer : 

Mark a new angle a°. 

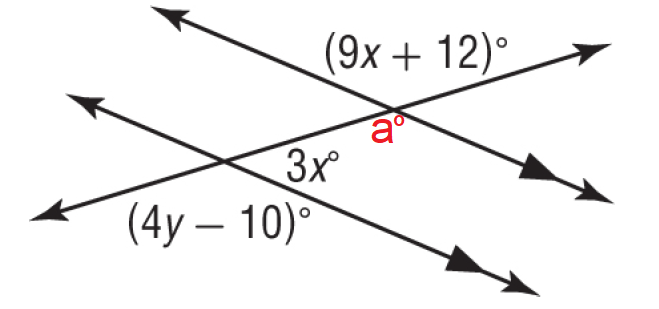
(9x + 12)° and a° are consecutive interior angles, they are supplementary.

a° + 3x°  =  180°

By Vertical Angles Theorem, a° = (9x + 12)°.  

(9x + 12)° + 3x°  =  180°

9x + 12 + 3x  =  180

12x + 12  =  180

Subtract 12 from each side. 

12x  =  168

Divide each side by 12.

x  =  14

(4y - 10)° and 3x° form a linear pair, they are supplementary.

(4y - 10)° + 3x°  =  180°

4y - 10 + 3x  =  180

Substitute x = 14.

4y - 10 + 3(14)  =  180

4y - 10 + 42  =  180

4y + 32  =  180

Subtract 32 from each side. 

4y  =  148

Divide each side by 4.

y  =  37

Therefore, 

x  =  14  and  y  =  37

7. Answer : 

Since the inscribed angle ∠WXY intercepts the diameter, it is a right angle.  

m∠WXY  =  90°

(13x - 1)°  =  90°

13x - 1  =  90

Add 1 to each side. 

13x  =  91

Divide each side by 13.

x  =  7

8. Answer : 

In the figure above,

m∠arc AC + 162° + 92°  =  360°

m∠arc AC + 254°  =  360°

Subtract 254° from each side. 

m∠arc AC  =  106°

The measure of an inscribed angle is equal to half of the measure of its intercepted arc.

m∠ABC  =  (1/2) ⋅ m∠arc AC

(7x - 10)°  =  (1/2) ⋅ 106°

(7x - 10)°  =  53°

7x - 10  =  53

Add 10 to each side. 

7x  =  63

Divide each side by 7.

x  =  9

9. Answer : 

In the figure above, two inscribed angles ∠ABD and ∠ACD intercept the same arc AD. Then, ∠ABD and ∠ACD are congruent. 

m∠ABD  =  m∠ACD

(6x + 26)°  =  (13x - 9)°

6x + 26  =  13x - 9

Subtract 6x from each side. 

26  =  7x - 9

Add 9 to each side. 

35  =  7x

Divide each side by 7.

5  =  x

10. Answer : 

Since the quadrilateral STUV is inscribed in a circle, its opposite angles are supplementary. 

m∠T + m∠V  =  180°

Substitute.

(62 - 5x)° + 133°  =  180°

62 - 5x + 133  =  180

195 - 5x  =  180

Subtract 195 from each side.

-5x  =  -15

Divide each side by -5.

x  =  3

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.