ADDITIVE INVERSE WORKSHEET

Problem 1 :

Find the additive inverse of '-15'. 

Problem 2 :

Find the additive inverse of '-0.3'. 

Problem 3 :

Find the additive inverse of '3'. 

Problem 4 :

Find the additive inverse of '1/7'. 

Problem 5 :

Simplify : 

(-9) + 9

Problem 6 :

Simplify : 

7 + (-7)

Problem 7 :

Given : 

5 + x  =  0

Problem 8 :

Given : 

(-7/8) + (x/8)  =  0

Problem 9 :

Given : 

(2/3) + (x/6)  =  0

Problem 10 : 

A football team loses 3.5 yards on their first play. On the next play, they gain 3.5 yards. What is the overall increase or decrease in yards ?

Detailed Answer Key

Problem 1 :

Find the additive inverse of '-15'. 

Solution :

The given number is a negative number.

Then, its additive inverse is the number itself with positive sign.

So, additive inverse of '-15' is

+15

Problem 2 :

Find the additive inverse of '-0.3'. 

Solution :

The given number is a negative number.

Then, its additive inverse is the number itself with positive sign.

So, additive inverse of '-0.3' is

+0.3

Problem 3 :

Find the additive inverse of '3'. 

Solution :

The given number is a positive number.

Then, its additive inverse is the number itself with negative sign.

So, additive inverse of '3' is

-3

Problem 4 :

Find the additive inverse of '1/7'. 

Solution :

The given number is a positive number.

Then, its additive inverse is the number itself with negative sign.

So, additive inverse of '1/7' is

-1/7

Problem 5 :

Simplify : 

(-9) + 9

Solution :

The numerical expression '(-9) + 9' is the sum of '-9' and its additive inverse '+9'.

We know the fact that the sum of a number and its additive inverse is zero. 

So, 

(-9) + 9  =  0

Problem 6 :

Simplify : 

7 + (-7)

Solution :

The numerical expression '7 + (-7)' is the sum of '7' and its additive inverse '-7'.

We know the fact that the sum of a number and its additive inverse is zero. 

So, 

7 + (-7)  =  0

Problem 7 :

Given : 

5 + x  =  0

Find the value of 'x'.

Solution :

It is given that the sum of '5' and 'x' is zero.

Then, additive inverse of '5' is 'x'. 

But, additive inverse of '5' is '-5'

So, 

x  =  -5

Problem 8 :

Given : 

(-7/8) + (x/8)  =  0

Find the value of 'x'.

Solution :

It is given that the sum of '-7/8' and 'x/8' is zero.

Then, additive inverse of '-7/8' is 'x/8'. 

But, additive inverse of '-7/8' is '7/8'

So, 

x/8  =  7/8

x  =  7

Problem 9 :

Given : 

(2/3) + (x/6)  =  0

Find the value of 'x'.

Solution :

It is given that the sum of '2/3' and 'x/6' is zero.

Then, additive inverse of '2/3' is 'x/6'. 

But, additive inverse of '2/3' is '-2/3'

So, 

x/6  =  -2/3

Multiply each side by 6.

x  =  -4

Problem 10 : 

A football team loses 3.5 yards on their first play. On the next play, they gain 3.5 yards. What is the overall increase or decrease in yards?

Solution : 

Step 1 : 

Use a positive number to represent the gain in yards and a negative number to represent the loss in yards.

Step 2 : 

Find -3.5 + 3.5.

Step 3 : 

Start at -3.5.

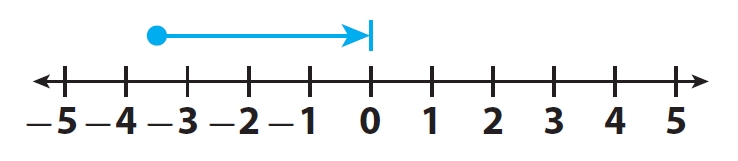
Step 4 : 

Move | 3.5 | = 3.5 units to the right, because the second addend is positive.

The result is 0.

This means the overall change is 0 yards.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.